Puzzle procrastination: perplexing probabilities part II

February 27, 2015 / CPLB / Leave a comment

A while ago I set some probability puzzles. If you’ve not yet pondered them, give them a whirl now. It’s OK, I’ll wait… All done? Final answer?

1 Girls, boys and doughnuts

We know that Laura has two children. There are four possibilities: two girls ( $\mathrm{GG}$ ), a boy and a girl ( $\mathrm{BG}$ ), a girl and a boy ( $\mathrm{GB}$ ) and two boys ( $\mathrm{BB}$ ). The probability of having a boy is almost identical to having a girl, so let’s keep things simple and assume that all four options have equal probability.

In this case, (i) the probability of having two girls is $P(\mathrm{GG}) = 1/4$ ; (ii) the probability of having a boy and a girl is $P(\mathrm{B,\,G}) = P(\mathrm{BG}) + P(\mathrm{GB}) = 1/2$ , and (iii) the probability of having two boys is $P(\mathrm{BB}) = 1/4$ .

After meeting Laura’s daughter Lucy, we know she doesn’t have two boys. What are the probabilities now? There are three options left ( $\mathrm{GG}$ , $\mathrm{GB}$ and $\mathrm{BG}$ ), but they are not all equally likely. We’ve discussed a similar problem before (it involved water balloons). You can work out the probabilities using Bayes’ Theorem, but let’s see if we can get away without using any maths more complicated than addition. Lucy could either be the elder or the younger child, each is equally likely. There must be four possible outcomes: Lucy and then another girl ( $\mathrm{LG}$ ), another girl and then Lucy ( $\mathrm{GL}$ ), Lucy and then a boy ( $\mathrm{LB}$ ) or a boy and then Lucy ( $\mathrm{BL}$ ). Since the sex of children are not linked (if we ignore the possibility of identical twins), each of these are equally probable. Therefore, (i) $P(\mathrm{GG}) = P(\mathrm{LG}) + P(\mathrm{GL}) = 1/2$ ; (ii) $P(\mathrm{B,\,G}) = P(\mathrm{LB}) + P(\mathrm{BL}) = 1/2$ , and (iii) $P(\mathrm{BB}) = 0$ . We have ruled out one possibility, and changed the probability having two girls.

If we learn that Lucy is the eldest, then we are left with two options, $\mathrm{LG}$ and $\mathrm{LB}$ . This means (i) $P(\mathrm{GG}) = P(\mathrm{LG}) = 1/2$ ; (ii) $P(\mathrm{B,\,G}) = P(\mathrm{LB}) = 1/2$ , and (iii) $P(\mathrm{BB}) = 0$ . The probabilities haven’t changed! This is because the order of birth doesn’t influence the probability of being a boy or a girl.

Hopefully that all makes sense so far. Now let’s move on to Laura’s secret society for people who have two children of which at least one is a girl. There are three possibilities for the children: $\mathrm{GG}$ , $\mathrm{BG}$ or $\mathrm{GB}$ . This time, all three are equally likely as we are just selecting them equally from the total population. Families with two children are equally likely to have each of the four combinations, but those with $\mathrm{BB}$ are turned away at the door, leaving an equal mix of the other three. Hence, (i) $P(\mathrm{GG}) = 1/3$ ; (ii) $P(\mathrm{B,\,G}) = P(\mathrm{BG}) + P(\mathrm{GB}) = 2/3$ , and (iii) $P(\mathrm{BB}) = 0$ .

The probabilities are different in this final case than for Laura’s family! This is because of the difference in the way we picked are sample. With Laura, we knew she had two children, the probability that she would have a daughter with her depends upon how many daughters she has. It’s more likely that she’d have a daughter with her if she has two, than one (or zero). If we’re picking families with at least one girl at random, things are different. This has confused enough people to be known as the boy or girl paradox. However, if you’re careful in writing things down, it’s not too tricky to work things out.

2 Do or do-nut

You’re eating doughnuts, and trying to avoid the one flavour you don’t like. After eating six of twenty-four you’ve not encountered it. The other guests have eaten twelve, but that doesn’t tell you if they’ve eaten it. All you know is that it’s not in the six you’ve eaten, hence it must be one of the other eighteen. The probability that one of the twelve that the others have eaten is the nemesis doughnut is $P(\mathrm{eaten}) = 12/18 = 2/3$ . Hence, the probability it is left is $P(\mathrm{left}) = 1 - P(\mathrm{eaten}) = 1/3$ . Since there are six doughnuts left, the probability you’ll pick the nemesis doughnut next is $P(\mathrm{next}) = P(\mathrm{left}) \times 1/6 = 1/18$ . Equally, you could have figured that out by realising that it’s equally probable that the nemesis doughnut is any of the eighteen that you’ve not eaten.

When twelve have been eaten, Lucy takes one doughnut to feed the birds. You all continue eating until there are four left. At this point, no-one has eaten that one doughnut. There are two possible options: either it’s still lurking or it’s been fed to the birds. Because we didn’t get to use it in the first part, I’ll use Bayes’ Theorem to work out the probabilities for both options.

The probability that Lucy luckily picked that one doughnut to feed to the birds is $P(\mathrm{lucky}) = 1/12$ , the probability that she unluckily picked a different flavour is $P(\mathrm{unlucky}) = 1 - P(\mathrm{lucky}) = 11/12$ . If we were lucky, the probability that we managed to get down to there being four left is $P(\mathrm{four}|\mathrm{lucky}) = 1$ , we were guaranteed not to eat it! If we were unlucky, that the bad one is amongst the remaining eleven, the probability of getting down to four is $P(\mathrm{four}|\mathrm{unlucky}) = 4/11$ . The total probability of getting down to four is

$P(\mathrm{four}) = P(\mathrm{four}|\mathrm{lucky})P(\mathrm{lucky}) + P(\mathrm{four}|\mathrm{unlucky})P(\mathrm{unlucky})$ .

Substituting in gives

$\displaystyle P(\mathrm{four}) = 1 \times \frac{1}{12} + \frac{4}{11} \times \frac{11}{12} = \frac{5}{12}$ .

The probability that the doughnut is not left is when there are four left is

$\displaystyle P(\mathrm{lucky}|\mathrm{four}) = \frac{P(\mathrm{four}|\mathrm{lucky})P(\mathrm{lucky})}{P(\mathrm{four})}$ ,

putting in the numbers gives

$\displaystyle P(\mathrm{lucky}|\mathrm{four}) = 1 \times \frac{1}{12} \times \frac{12}{5} = \frac{1}{5}$ .

The probability that it’s left must be

$\displaystyle P(\mathrm{unlucky}|\mathrm{four}) = \frac{4}{5}$ .

We could’ve worked this out more quickly by realised that there are five doughnuts that could potential be the one: the four left and the one fed to the birds. Each one is equally probable, so that gives $P(\mathrm{lucky}|\mathrm{four}) = 1/5$ and $P(\mathrm{unlucky}|\mathrm{four}) = 4/5$ .

If you take one doughnut each, one after another, does it matter when you pick? You have an equal probability of each being the one. The probability that it’s the first is

$\displaystyle P(\mathrm{first}) = \frac{1}{4} \times P(\mathrm{unlucky}|\mathrm{four}) = \frac{1}{5}$ ;

the probability that it’s the second is

$\displaystyle P(\mathrm{second}) = \frac{1}{3} \times \frac{3}{4} \times P(\mathrm{unlucky}|\mathrm{four}) = \frac{1}{5}$ ;

the probability that it’s the third is

$\displaystyle P(\mathrm{third}) = \frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times P(\mathrm{unlucky}|\mathrm{four}) = \frac{1}{5}$ ,

and the probability that it’s the fourth (last) is

$\displaystyle P(\mathrm{third}) = 1 \times \frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times P(\mathrm{unlucky}|\mathrm{four}) = \frac{1}{5}$ .

That doesn’t necessarily mean it doesn’t matter when you pick though! That really depends how you feel when taking an uncertain bite, how much you value the knowledge that you can safely eat your doughnut, and how you’d feel about skipping your doughnut rather than eating one you hate.

Puzzle procrastination: perplexing probabilities

November 2, 2014February 27, 2015 / CPLB / Leave a comment

I enjoy pondering over puzzles. Figuring out correct probabilities can be confusing, but it is a good exercise to practise logical reasoning. Previously, we have seen how to update probabilities when given new information; let’s see if we use this to solve some puzzles!

1 Girls, boys and doughnuts

As an example, we’ve previously calculated the probabilities for the boy–girl distribution of our office-mate Iris’ children. Let’s imagine that we’ve popped over to Iris’ for doughnuts (this time while her children are out), and there we meet her sister Laura. Laura tells us that she has two children. What are the probabilities that Laura has: (i) two girls, (ii) a girl and a boy, or (iii) two boys?

It turns out that Laura has one of her children with her. After you finish your second doughnut (a chocolatey, custardy one), Laura introduces you to her daughter Lucy. Lucy loves LEGO, but that is unimportant for the current discussion. How does Lucy being a girl change the probabilities?

While you are finishing up your third doughnut (with plum and apple jam), you discover that Lucy is the eldest child. What are the probabilities now—have they changed?

Laura is a member of an extremely selective club for mothers with two children of which at least one is a girl. They might fight crime at the weekends, Laura gets a little evasive about what they actually do. What are the probabilities that a random member of this club has (i) two girls, (ii) a girl and a boy, or (iii) two boys?

The answers to similar questions have been the subject to lots of argument, even though they aren’t about anything too complicated. If you figure out the answers, you might see how the way you phrase the question is important.

2 Do or do-nut

You are continuing to munch through the doughnuts at Iris’. You are working your way through a box of 24. There is one of each flavour and you know there is one you do not like (which we won’t mention for liable reasons). There’s no way of telling what flavour a doughnut is before biting into it. You have now eaten six, not one of which was the bad one. The others have eaten twelve between them. What is the probability that your nemesis doughnut is left? What is the probability that you will pick it up next?

You continue munching, as do the others. You discover that Iris, Laura and Lucy all hate the same flavour that you do, but that none of them have eaten it. There are now just four doughnuts left. Lucy admits that she did take one of the doughnuts to feed the birds in the garden (although they didn’t actually eat it as they are trying to stick to a balanced diet). She took the doughnut while there were still 12 left. What is the probability that the accursed flavour is still lurking amongst the final four?

You are agree to take one each, one after another. Does it matter when you pick yours?

Happy pondering! I shall post the solutions later.

An introduction to probability: Inference and learning from data

October 18, 2014February 7, 2015 / CPLB / Leave a comment

Probabilities are a way of quantifying your degree of belief. The more confident you are that something is true, the larger the probability assigned to it, with 1 used for absolute certainty and 0 used for complete impossibility. When you get new information that updates your knowledge, you should revise your probabilities. This is what we do all the time in science: we perform an experiment and use our results to update what we believe is true. In this post, I’ll explain how to update your probabilities, just as Sherlock Holmes updates his suspicions after uncovering new evidence.

Taking an umbrella

Imagine that you are a hard-working PhD student and you have been working late in your windowless office. Having finally finished analysing your data, you decide it’s about time to go home. You’ve been trapped inside so long that you no idea what the weather is like outside: should you take your umbrella with you? What is the probability that it is raining? This will depend upon where you are, what time of year it is, and so on. I did my PhD in Cambridge, which is one of the driest places in England, so I’d be confident that I wouldn’t need one. We’ll assume that you’re somewhere it doesn’t rain most of the time too, so at any random time you probably wouldn’t need an umbrella. Just as you are about to leave, your office-mate Iris comes in dripping wet. Do you reconsider taking that umbrella? We’re still not certain that it’s raining outside (it could have stopped, or Iris could’ve just been in a massive water-balloon fight), but it’s now more probable that it is raining. I’d take the umbrella. When we get outside, we can finally check the weather, and be pretty certain if it’s raining or not (maybe not entirely certain as, after plotting that many graphs, we could be hallucinating).

In this story we get two new pieces of information: that newly-arrived Iris is soaked, and what we experience when we get outside. Both of these cause us to update our probability that it is raining. What we learn doesn’t influence whether it is raining or not, just what we believe regarding if it is raining. Some people worry that probabilities should be some statement of absolute truth, and so because we changed our probability of it raining after seeing that our office-mate is wet, there should be some causal link between office-mates and the weather. We’re not saying that (you can’t control the weather by tipping a bucket of water over your office-mate), our probabilities just reflect what we believe. Hopefully you can imagine how your own belief that it is raining would change throughout the story, we’ll now discuss how to put this on a mathematical footing.

Bayes’ theorem

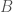We’re going to venture into using some maths now, but it’s not too serious. You might like to skip to the example below if you prefer to see demonstrations first. I’ll use $P(A)$ to mean the probability of $A$ . A joint probability describes the probability of two (or more things), so we have $P(A, B)$ as the probability that both $A$ and $B$ happen. 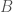The probability that $A$ happens given that $B$ happens is the conditional probability $P(A|B)$ . 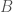Consider the the joint probability of $A$ and $B$ : we want both to happen. We could construct this in a couple of ways. First we could imagine that $A$ happens, and then $B$ . 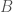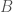In this case we build up the joint probability of both by working out the probability that $A$ happens and then the probability $B$ happens given $A$ . Putting that in equation form

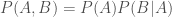$P(A,B) = P(A)P(B|A)$ .

Alternatively, we could have 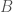$B$ first and then $A$ . This gives us a similar result of

$P(A,B) = P(B)P(A|B)$ .

Both of our equations give the same result. (We’ve checked this before). If we put the two together then

$P(B|A)P(A) = P(A|B)P(B)$ .

Now we divide both sides by $P(A)$ and bam:

$\displaystyle P(B|A) = \frac{P(A|B)P(B)}{P(A)}$ ,

this is Bayes’ theorem. I think the Reverend Bayes did rather well to get a theorem named after him for noting something that is true and then rearranging! We use Bayes’ theorem to update our probabilities.

Usually, when doing inference (when trying to learn from some evidence), we have some data (that our office-mate is damp) and we want to work out the probability of our hypothesis (that it’s raining). We want to calculate $P(\mathrm{hypothesis}|\mathrm{data})$ . We normally have a model that can predict how likely it would be to observe that data if our hypothesis is true, so we know $P(\mathrm{data}|\mathrm{hypothesis})$ , so we just need to convert between the two. This is known as the inverse problem.

We can do this using Bayes’ theorem

$\displaystyle P(\mathrm{hypothesis}|\mathrm{data}) = \frac{P(\mathrm{data}|\mathrm{hypothesis})P(\mathrm{hypothesis})}{P(\mathrm{data})}$ .

In this context, we give names to each of the probabilities (to make things sound extra fancy): $P(\mathrm{hypothesis}|\mathrm{data})$ is the posterior, because it’s what we get at the end; $P(\mathrm{data}|\mathrm{hypothesis})$ is the likelihood, it’s what you may remember calculating in statistics classes; 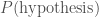$P(\mathrm{hypothesis})$ is the prior, because it’s what we believed about our hypothesis before we got the data, and $P(\mathrm{data})$ is the evidence. If ever you hear of someone doing something in a Bayesian way, it just means they are using the formula above. I think it’s rather silly to point this out, as it’s really the only logical way to do science, but people like to put “Bayesian” in the title of their papers as it sounds cool.

Whenever you get some new information, some new data, you should update your belief in your hypothesis using the above. The prior is what you believed about hypothesis before, and the posterior is what you believe after (you’ll use this posterior as your prior next time you learn something new). There are a couple of examples below, but before we get there I will take a moment to discuss priors.

About priors: what we already know

There have been many philosophical arguments about the use of priors in science. People worry that what you believe affects the results of science. Surely science should be above such things: it should be about truth, and should not be subjective! Sadly, this is not the case. Using Bayes’ theorem is the only logical thing to do. You can’t calculate a probability of what you believe after you get some data unless you know what you believed beforehand. If this makes you unhappy, just remember that when we changed our probability for it being raining outside, it didn’t change whether it was raining or not. If two different people use two different priors they can get two different results, but that’s OK, because they know different things, and so they should expect different things to happen.

To try to convince yourself that priors are necessary, consider the case that you are Sherlock Holmes (one of the modern versions), and you are trying to solve a bank robbery. There is a witness who saw the getaway, and they can remember what they saw with 99% accuracy (this gives the likelihood). If they say the getaway vehicle was a white transit van, do you believe them? What if they say it was a blue unicorn? In both cases the witness is the same, the likelihood is the same, but one is much more believable than the other. My prior that the getaway vehicle is a transit van is much greater than my prior for a blue unicorn: the latter can’t carry nearly as many bags of loot, and so is a silly choice.

If you find that changing your prior (to something else sensible) significantly changes your results, this just means that your data don’t tell you much. Imagine that you checked the weather forecast before leaving the office and it said “cloudy with 0–100% chance of precipitation”. You basically believe the same thing before and after. This really means that you need more (or better) data. I’ll talk about some good ways of calculating priors in the future.

Solving the inverse problem

Example 1: Doughnut allergy

We shall now attempt to use Bayes’ theorem to calculate some posterior probabilities. First, let’s consider a worrying situation. Imagine there is a rare genetic disease that makes you allergic to doughnuts. One in a million people have this disease, that only manifests later in life. You have tested positive. The test is 99% successful at detecting the disease if it is present, and returns a false positive (when you don’t have the disease) 1% of the time. How worried should you be? Let’s work out the probability of having the disease given that you tested positive

$\displaystyle P(\mathrm{allergy}|\mathrm{positive}) = \frac{P(\mathrm{positive}|\mathrm{allergy})P(\mathrm{allergy})}{P(\mathrm{positive})}$ .

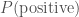Our prior for having the disease is given by how common it is, $P(\mathrm{allergy}) = 10^{-6}$ . The prior probability of not having the disease is $P(\mathrm{no\: allergy}) = 1 - P(\mathrm{allergy})$ . The likelihood of our positive result is $P(\mathrm{positive}|\mathrm{allergy}) = 0.99$ , which seems worrying. The evidence, the total probability of testing positive $P(\mathrm{positive})$ is found by adding the probability of a true positive and a false positive

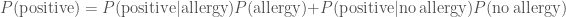$P(\mathrm{positive}) = P(\mathrm{positive}|\mathrm{allergy})P(\mathrm{allergy}) + P(\mathrm{positive}|\mathrm{no\: allergy})P(\mathrm{no\: allergy})$ .

The probability of a false positive is $P(\mathrm{positive}|\mathrm{no\: allergy}) = 0.01$ . We thus have everything we need. Substituting everything in, gives

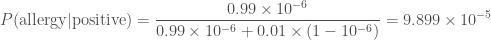$\displaystyle P(\mathrm{allergy}|\mathrm{positive}) = \frac{0.99 \times 10^{-6}}{0.99 \times 10^{-6} + 0.01 \times (1 - 10^{-6})} = 9.899 \times 10^{-5}$ .

Even after testing positive, you still only have about a one in ten thousand chance of having the allergy. While it is more likely that you have the allergy than a random member of the public, it’s still overwhelmingly probable that you’ll be fine continuing to eat doughnuts. Hurray!

Doughnut love: probably fine.

Example 2: Boys, girls and water balloons

Second, imagine that Iris has three children. You know she has a boy and a girl, but you don’t know if she has two boys or two girls. You pop around for doughnuts one afternoon, and a girl opens the door. She is holding a large water balloon. What’s the probability that Iris has two girls? We want to calculate the posterior

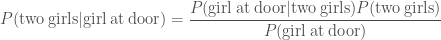$\displaystyle P(\mathrm{two\: girls}|\mathrm{girl\:at\:door}) = \frac{P(\mathrm{girl\:at\:door}|\mathrm{two\: girls})P(\mathrm{two\: girls})}{P(\mathrm{girl\:at\:door})}$ .

As a prior, we’d expect boys and girls to be equally common, so $P(\mathrm{two\: girls}) = P(\mathrm{two\: boys}) = 1/2$ . If we assume that it is equally likely that any one of the children opened the door, then the likelihood that one of the girls did so when their are two of them is $P(\mathrm{girl\:at\:door}|\mathrm{two\: girls}) = 2/3$ . Similarly, if there were two boys, the probability of a girl answering the door is $P(\mathrm{girl\:at\:door}|\mathrm{two\: boys}) = 1/3$ . The evidence, the total probability of a girl being at the door is

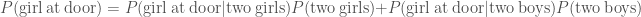$P(\mathrm{girl\:at\:door}) =P(\mathrm{girl\:at\:door}|\mathrm{two\: girls})P(\mathrm{two\: girls}) +P(\mathrm{girl\:at\:door}|\mathrm{two\: boys}) P(\mathrm{two\: boys})$ .

Using all of these,

$\displaystyle P(\mathrm{two\: girls}|\mathrm{girl\:at\:door}) = \frac{(2/3)(1/2)}{(2/3)(1/2) + (1/3)(1/2)} = \frac{2}{3}$ .

Even though we already knew there was at least one girl, seeing a girl first makes it much more likely that the Iris has two daughters. Whether or not you end up soaked is a different question.

Example 3: Fudge!

Finally, we shall return to the case of Ted and his overconsumption of fudge. Ted claims to have eaten a lethal dose of fudge. Given that he is alive to tell the anecdote, what is the probability that he actually ate the fudge? Here, our data is that Ted is alive, and our hypothesis is that he did eat the fudge. We have

$\displaystyle P(\mathrm{fudge}|\mathrm{survive}) = \frac{P(\mathrm{survive}|\mathrm{fudge})P(\mathrm{fudge})}{P(\mathrm{survive})}$ .

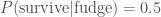This is a case where our prior, the probability that he would eat a lethal dose of fudge $P(\mathrm{fudge})$ , makes a difference. We know the probability of surviving the fatal dose is $P(\mathrm{survive}|\mathrm{fudge}) = 0.5$ . The evidence, the total probability of surviving $P(\mathrm{survive})$ , is calculated by considering the two possible sequence of events: either Ted ate the fudge and survived or he didn’t eat the fudge and survived

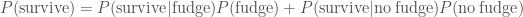$P(\mathrm{survive}) = P(\mathrm{survive}|\mathrm{fudge})P(\mathrm{fudge}) + P(\mathrm{survive}|\mathrm{no\: fudge})P(\mathrm{no\: fudge})$ .

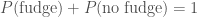We’ll assume if he didn’t eat the fudge he is guaranteed to be alive, $P(\mathrm{survive}| \mathrm{no\: fudge}) = 1$ . Since Ted either ate the fudge or he didn’t $P(\mathrm{fudge}) + P(\mathrm{no\: fudge}) = 1$ . Therefore,

$P(\mathrm{survive}) = 0.5 P(\mathrm{fudge}) + [1 - P(\mathrm{fudge})] = 1 - 0.5 P(\mathrm{fudge})$ .

This gives us a posterior

$\displaystyle P(\mathrm{fudge}|\mathrm{survive}) = \frac{0.5 P(\mathrm{fudge})}{1 - 0.5 P(\mathrm{fudge})}$ .

We just need to decide on a suitable prior.

If we believe Ted could never possibly lie, then he must have eaten that fudge and $P(\mathrm{fudge}) = 1$ . In this case,

$\displaystyle P(\mathrm{fudge}|\mathrm{survive}) = \frac{0.5}{1 - 0.5} = 1$ .

Since we started being absolutely sure, we end up being absolutely sure: nothing could have changed our mind! This is a poor prior: it is too strong, we are being closed-minded. If you are closed-minded you can never learn anything new.

If we don’t know who Ted is, what fudge is, or the ease of consuming a lethal dose, then we might assume an equal prior on eating the fudge and not eating the fudge, $P(\mathrm{fudge}) = 0.5$ . In this case we are in a state of ignorance. Our posterior is

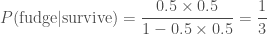$\displaystyle P(\mathrm{fudge}|\mathrm{survive}) = \frac{0.5 \times 0.5}{1 - 0.5 \times 0.5} = \frac{1}{3}$ .

Even though we know nothing, we conclude that it’s more probable that the Ted did not eat the fudge. In fact, it’s twice as probable that he didn’t eat the fudge than he did as $P(\mathrm{no\: fudge}|\mathrm{survive}) = 1 -P(\mathrm{fudge}|\mathrm{survive}) = 2/3$ .

In reality, I think that it’s extremely improbable anyone could consume a lethal dose of fudge. I’m fairly certain that your body tries to protect you from such stupidity by expelling the fudge from your system before such a point. However, I will concede that it is not impossible. I want to assign a small probability to $P(\mathrm{fudge})$ . I don’t know if this should be one in a thousand, one in a million or one in a billion, but let’s just say it is some small value $p$ . Then

$\displaystyle P(\mathrm{fudge}|\mathrm{survive}) = \frac{0.5 p}{1 - 0.5 p} \approx 0.5 p$ .

as the denominator is approximately one. Whatever small probability I pick, it is half as probable that Ted ate the fudge.

I would assign a much higher probability to Mr. Impossible being able to eat that much fudge than Ted.

While it might not be too satisfying that we can’t come up with incontrovertible proof that Ted didn’t eat the fudge, we might be able to shut him up by telling him that even someone who knows nothing would think his story is unlikely, and that we will need much stronger evidence before we can overcome our prior.

Homework example: Monty Hall

You now have all the tools necessary to tackle the Monty Hall problem, one of the most famous probability puzzles:

You are on a game show and are given the choice of three doors. Behind one is a car (a Lincoln Continental), but behind the others are goats (which you don’t want). You pick a door. The host, who knows what is behind the doors, opens another door to reveal goat. They then offer you the chance to switch doors. Should you stick with your current door or not? — Monty Hall problem

You should be able to work out the probability of winning the prize by switching and sticking. You can’t guarantee you win, but you can maximise your chances.

Summary

Whenever you encounter new evidence, you should revise how probable you think things are. This is true in science, where we perform experiments to test hypotheses; it is true when trying to solve a mystery using evidence, or trying to avoid getting a goat on a game show. Bayes’ theorem is used to update probabilities. Although Bayes’ theorem itself is quite simple, calculating likelihoods, priors and evidences for use in it can be difficult. I hope to return to all these topics in the future.

On symmetry

August 13, 2014October 25, 2014 / CPLB / Leave a comment

Dave Green only combs half of his beard, the rest follows by symmetry. — Dave Green Facts

Physicists love symmetry! Using symmetry can dramatically simplify a problem. The concept of symmetry is at the heart of modern theoretical physics and some of the most beautiful of scientific results.

In this post, I’ll give a brief introduction to how physicists think about symmetry. Symmetry can be employed in a number of ways when tackling a problem; we’ll have a look at how they can help you ask the right question and then check that your answer makes sense. In a future post I hope to talk about Noether’s Theorem, my all-time favourite result in theoretical physics, which is deeply entwined with the concept of symmetry. First, we shall discuss what we mean when we talk about symmetry.

What is symmetry?

We say something is symmetric with respect to a particular operation if it is unchanged after that operation. That might sound rather generic, but that’s because the operation can be practically anything. Let’s consider a few examples:

Possibly the most familiar symmetry would be reflection symmetry, when something is identical to its mirror image. Something has reflection symmetry if it is invariant under switching left and right. Squares have reflection symmetry along lines in the middle of their sides and along their diagonals, rectangles only have reflection symmetry along the lines in the middle of their sides, and circles have reflection symmetry through any line that goes through their centre.
The Star Trek Mirror Universe actually does not have reflection symmetry with our own Universe. First, they switch good and evil, rather than left and right, and second, after this transformation, we can tell the two universes apart by checking Spock’s beard.
Rotational symmetry is when an object is identical after being rotated. Squares are the same after a 90° rotation, rectangles are the same after a 180° rotation, and circles are the same after a rotation by any angle. There is a link between the rotational symmetry of these shapes and their mirror symmetry: you can combine two reflections to make a rotation. With rotations we have seen that symmetries can either be discrete, as for a square when we have to rotate by multiples of 90°, or continuous, as for the circle where we can pick any angle we like.
Translational symmetry is similar to rotational symmetry, but is when an object is the same when shifted along a particular direction. This could be a spatial direction, so shifting everything to the left, or in time. This are a little more difficult to apply to the real world than the simplified models that physicists like to imagine.
For translational invariance, imagine an infinite, flat plane, the same in all directions. This would be translational invariant in any direction parallel to the ground. It would be a terrible place to lose your keys. If you can imagine an infinite blob of tangerine jelly, that is entirely the same in all directions, we can translate in any direction we like. We think the Universe is pretty much like this on the largest scales (where details like galaxies are no longer important), except, it’s not quite as delicious.
The backgrounds in some Scooby-Doo cartoons show periodic translational invariance: they repeat on a loop, so if you translate by the right amount they are the same. This is a discrete symmetry, just like rotating my a fixed angle. Similarly, if you have a rigid daily routine, such that you do the same thing at the same time every day, then your schedule is symmetric with respect to a time translation of 24 hours.
Exchange symmetry is when you can swap two (or more) things. If you are building a LEGO model, you can switch two bricks of the same size and colour and end up with the same result, hence it is symmetric under the exchange of those bricks. The idea that we have the same physical system when we swap two particles, like two electrons, is important in quantum mechanics. In my description of translational symmetry, I could have equally well have used lime jelly instead of tangerine, or even strawberry, hence the argument is symmetric under exchange of flavours. The symmetry is destroyed should we eat the infinite jelly Universe (we might also get stomach ache).
Mario and Luigi are not symmetric under exchange, as anyone who has tried to play multiplayer Super Mario Bros. will know, as Luigi is the better jumper and has the better moustache.

There are lots more potential symmetries. Some used by physicists seem quite obscure, such as Lorentz symmetry, but the important thing to remember is that a symmetry of a system means we get the same thing back after a transformation.

Sometimes we consider approximate symmetries, when something is almost the same under a transformation. Coke and Pepsi are approximately exchange symmetric: try switching them for yourself. They are similar, but it is possible to tell them apart. The Earth has approximate rotational symmetry, but it is not exact as it is lumpy. The spaceship at the start of Spaceballs has approximate translational invariance: it just keeps going and going, but the symmetry is not exact as it does end eventually, so the symmetry only applies to the middle.

How to use symmetry

When studying for an undergraduate degree in physics, one of the first things you come to appreciate is that some coordinate systems make problems much easier than others. Coordinates are the set of numbers that describe a position in some space. The most familiar are Cartesian coordinates, when you use $x$ and $y$ to describe horizontal and vertical position respectively. Cartesian coordinates give you a nice grid with everything at right-angles. Undergrad students often like to stick with Cartesian coordinates as they are straight-forward and familiar. However, they can be a pain when describing a circle. If we want to plot a line five units from the origin of of coordinate system $(0,\,0)$ , we have to solve $\sqrt{x^2 + y^2} = 5$ . However, if we used a polar coordinate system, it would simply be $r = 5$ . By using coordinates that match the symmetry of our system we greatly simplify the problem!

Pirates are trying to figure out where they buried their treasure. They know it’s 5 yarrrds from the doughnut. Calculating positions using Cartesian coordinates is difficult, but they are good for specifying specific locations, like of the palm tree.

Using polar coordinates, it is easy to specify the location of points 5 yarrrds from the doughnut. Pirates prefer using the polar coordinates, they really like using r.

Picking a coordinate system for a problem should depend on the symmetries of the system. If we had a system that was translation invariant, Cartesian coordinates are the best to use. If the system was invariant with respect to translation in the horizontal direction, then we know that our answer should not depend on $x$ . If we have a system that is rotation invariant, polar coordinates are the best, as we should get an answer that doesn’t depend on the rotation angle $\varphi$ . By understanding symmetries, we can formulate our analysis of the problem such that we ask the best questions.

At the end of my undergrad degree, my friends and I went along to an awards ceremony. I think we were hoping they’d have the miniature éclairs they normally had for special occasions. There was a chap from an evil corporation™ giving away branded clocks, that apparently ran on water. We were fairly convinced there was more to it than that, so, as now fully qualified physicists, we though we should able to figure it out. We quickly came up with two ideas: that there was some powder inside the water tank that reacted with the water to produce energy, or that the electrodes reacted in a similar way to in a potato clock. We then started to argue about how to figure this out. At this point, Peter Littlewood, then head of the Cavendish Laboratory, wandered over. We explained the problem, but not our ideas. Immediately, he said that it must be to do with the electrodes due to symmetry. Current flows to power the clock. It’ll either flow left to right through the tank, or right to left. It doesn’t matter which, but the important thing is the clock can’t have reflection symmetry. If it did, there would be no preferred direction for the current to flow. To break the symmetry, the two (similar looking) electrodes must actually be different (and hence the potato clock theory is along the right lines). My friends and I all felt appropriately impressed and humbled, but it served as a good reminder that a simple concept like symmetry can be a powerful tool.

A concept I now try to impress upon my students, is to use symmetry to guide their answers. Most are happy enough to use symmetry for error checking: if the solution is meant to have rotational symmetry and their answer depends on $\varphi$ they know they’ve made a mistake. However, symmetry can sometimes directly tell you the answer.

Lets imagine that you’ve baked a perfectly doughnut, such that it has rotational symmetry. For some reason you sprinkled it with an even coating of electrons instead of hundreds and thousands. We now want to calculate the electric field surrounding the doughnut (for obvious reasons). The electric field tells us which way charges are pushed/pulled. We’d expect positive charges to be attracted towards our negatively charged doughnut. There should be a radial electric field to pull positive charges in, but since it has rotational symmetry, there shouldn’t be any field in the $\varphi$ direction, as there’s now reason for charges to be pulled clockwise or anticlockwise round our doughnut. Therefore, we should be able to write down immediately that the electric field in the $\varphi$ direction is zero, by symmetry.

Most undergrads, though, will feel that this is cheating, and will often attempt to do all the algebra (hopefully using polar coordinates). Some will get this wrong, although there might be a few who are smart enough to note that their answer must be incorrect because of the symmetry. If symmetry tells you the answer, use it! Although it is good to practise your algebra (you get better by training), you can’t learn anything more than you already knew by symmetry. Working efficiently isn’t cheating, it’s smart.

Symmetry is a useful tool for problem solving, and something that everyone should make use of.

Christopher Berry

Gravitational-wave astronomer

doughnuts

Puzzle procrastination: perplexing probabilities part II

1 Girls, boys and doughnuts

2 Do or do-nut

Puzzle procrastination: perplexing probabilities

1 Girls, boys and doughnuts

2 Do or do-nut

An introduction to probability: Inference and learning from data

Taking an umbrella

Bayes’ theorem

About priors: what we already know