GW190521—The big one

September 2, 2020June 28, 2021 / CPLB / 3 Comments

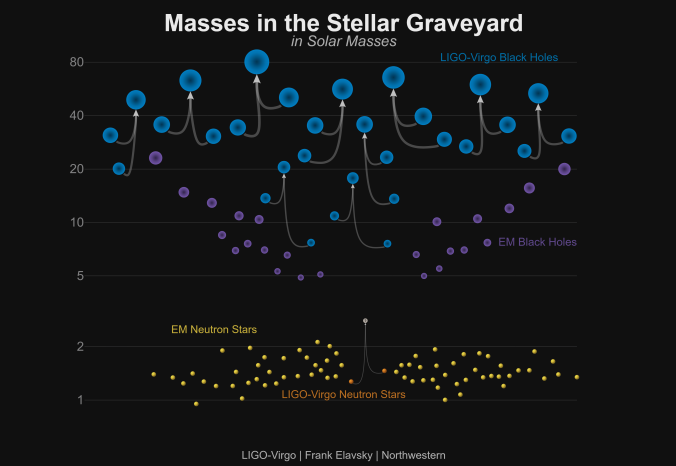
GW190521 is a huge discovery—it a gravitational wave signal from the coalescence of two black holes to form one about $140 M_\odot$ (where our Sun has a mass of $1 M_\odot$ ). That is the largest black hole we have yet discovered with gravitational waves. It is the first definitive discovery of an intermediate-mass black hole. It is also a puzzle, as it is a mystery how its source could form…

How big can a black hole be?

Anything can become a black hole if it is squeezed enough [bonus note]: you just need to pack enough stuff into a small enough space (just like when taking a Ryanair flight). In practice, most stuff is stiff enough to push back against squeezing to avoid becoming a black hole. It’s only when you get the core of a star about somewhere between $2.1 M_\odot$ and $3 M_\odot$ that gravity becomes strong enough to collapse things down to a black hole [bonus note]. Above this threshold, can we have a black hole of any size?

The biggest black holes are found in the centres of galaxies. These can be hundreds of thousands to tens of billions the mass of our Sun. Our own Milky Way has a rather moderate $4 \times 10^6 M_\odot$ black hole. These massive (or supermassive) black holes are far bigger than any star. Even Elvis. They therefore couldn’t have formed from a collapsing star. So how did they form? The truth is that we’re not sure. It’s possible that we started with smaller black holes and fed them up, or merged them together, or a mixture of both. These initial seed black holes could have formed from stars, or possibly giant clouds of collapsing gas (which may form $10,000 M_\odot$ black holes). In any case, whatever mechanism created these black holes needs to work quickly, as we know from observations of quasars, that there are massive black holes by the time the Universe is a mere billion years old. To figure out how massive black holes form, we need to discovery their seeds.

The Event Horizon Telescope's image of M87*

The shadow of a black hole reconstructed from the radio observations of the Event Horizon Telescope. The black hole lies at the centre of M87, and is about $6.5 \times 10^9 M_\odot$ . Credit: Event Horizon Team

Between stellar-mass black holes and massive black holes should lie intermediate-mass black holes. These are typically defined as having masses between $100 M_\odot$ and $100,000 M_\odot$ . Massive black holes should grow from these smaller black holes. However, we have never found one, they are the missing link in the black hole spectrum. There are candidates: ultrabright X-ray sources, or globular clusters with suspiciously moving stars, but none of these is rock solid, and couldn’t be explained another way. GW190521 changes this, at $142^{+28}_{-16} M_\odot$ the merger remnant is without doubt an intermediate-mass black hole.

This discovery shows that intermediate-mass black holes can form from mergers of smaller black holes. However, this doesn’t yet solve the mystery of how massive black holes are grown; we need observations of larger intermediate-mass black holes for that. We’ll keep searching.

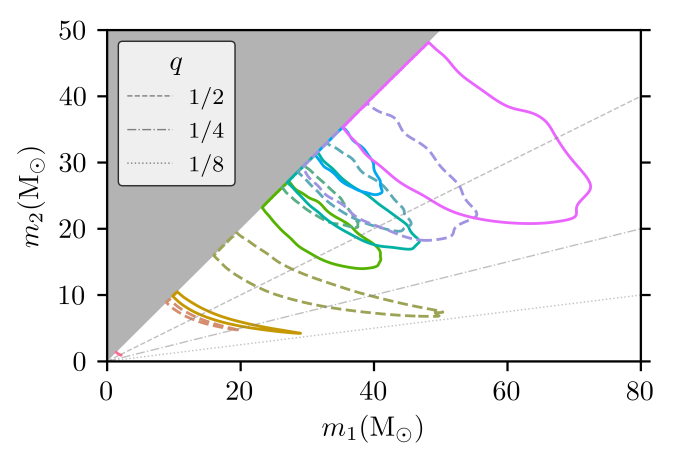
What I find more exciting about GW190521 are the masses of the two black holes that merged. Our analysis gives these as $85^{+21}_{-14} M_\odot$ and $66^{+17}_{-18} M_\odot$ . The large black hole masses extremely difficult to explain.

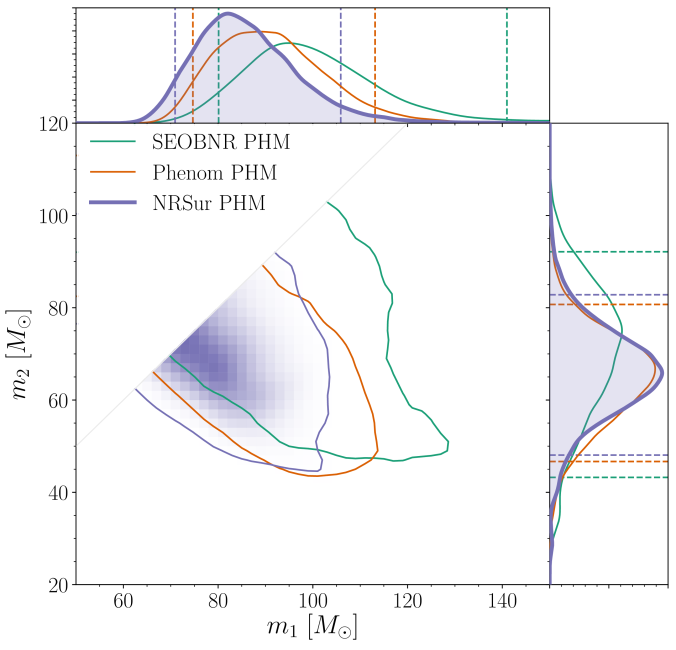
Estimated masses for the two components in the binary $m_1 \geq m_2$ . We show results several different waveform models and use the numerical relativity surrogate (NRSur PHM) as our best results. The two-dimensional shows the 90% probability contour. The dotted lines in one-dimensional plots the symmetric 90% credible interval. Part of Figure 1 of the GW190521 Implications Paper.

When you form a black hole from a star, its mass depends upon the mass of of its parent star. More massive stars generally form bigger black holes, but because of all the physics that goes on inside stars, it’s not a simple relationship. One important phenomena in determining the fate of massive stars is pair instability. When the cores of stars become very hot ( $\sim 3 \times 10^9~\mathrm{K}$ , just slightly less than the temperature of the mozerlla on that first bite of pizza, even though you should know better by now), the photons of light (gamma-rays) bouncing around inside the core become energetic enough to produce pairs of electrons and positrons [bonus note]. For the star, this causes some trouble. Its core is mostly supported by radiation pressure. If photons start disappearing as they are converted to electrons and positrons, then there isn’t as much radiation around, and the star will start to collapse. As it collapses, explosive nuclear reactions are triggered. Pair instability kicks in for stars with helium cores about $30 M_\odot$ . If the core is between $30 M_\odot$ and about $65 M_\odot$ , the star will blast off its outer layers, possibly repeating the cycle of pair-instability collapse and explosion many times. This results in smaller black holes than you might otherwise expect. For helium cores between $65 M_\odot$ and about $135 M_\odot$ , the explosion completely destroys the star, leaving nothing behind. These stars never collapse down to a black hole, and this leaves a gap, predicted to start somewhere between $45 M_\odot$ and $55 M_\odot$ .

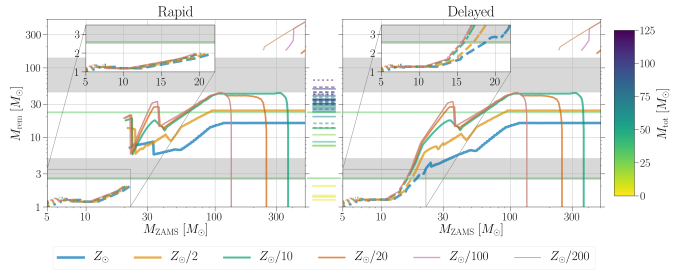
Remnant masses for stars of different masses

Remnant (white dwarf, neutron star or black hole) mass $M_\mathrm{rem}$ for different initial (zero age main sequence) stellar masses $M_\mathrm{ZAMS}$ . This is just for single stars, and ignores all the complicated things that can happen in binaries. The different coloured lines indicate different metallicities $Z$ (higher metallicity stars lose more mass through stellar winds). The two panels are for two different supernova models. The grey bars indicate potential mass gaps: the lower core collapse mass gap (only predicted by the Rapid model) and the upper pair-instability mass gap. The tick marks in the middle are various claimed gravitational-wave source, colour-coded by the total mass of the binary $M_\mathrm{tot}$ . Figure 1 of Zevin et al. (2020).

The more massive of GW190521’s black holes sits squarely in the expected pair-instability mass gap. How can we form such a system?

To delve into all the details, we have put together two papers on GW190521. The high mass of the system poses challenges not just for our understanding of astrophysics, but also for our data analysis. Below, I’ll go through what we have discovered.

The signal

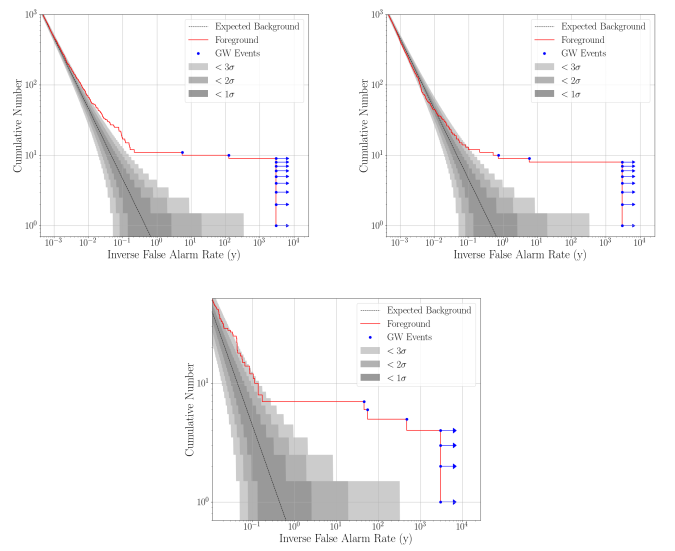
GW190521 was first identified in our online searches about 20 seconds after we took the data. All three of our detectors were online and observing at the time. It was a short bleep of a signal indicating a high mass system. Short signals always make me suspicious as they can easily confused with some types of glitch. The signal was picked up by multiple search algorithms, which generally is a good sign, as they all estimate the background of noise in a slightly different way. However, the estimated false alarm rates were only one per few years. That’s not terribly impressive—it’s the range where things can change as we collect more data. Immediately, checks of the signal began. We have many ways of monitoring our detectors, and experts started running through these. Microphones at Hanford picked up a helicopter overhead a few minutes later, but that’s too far away in time to be related to the signal. The initial checks all looked OK, so we were confident that it was safe to share the candidate detection S190521g.

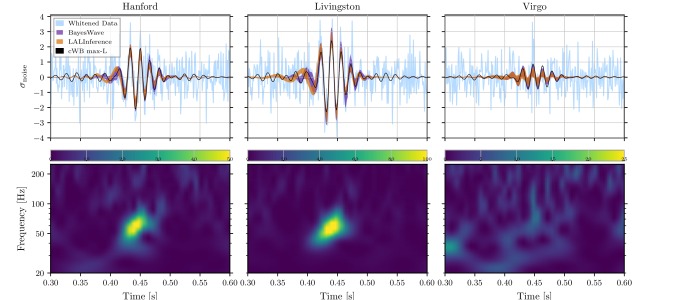
Visualisations of GW190521. The top panels show whitened data and reconstructed waveforms from the template-free detection algorithm cWB, BayesWave (which reconstructs the signal from sine–Gaussian wavelets), and our parameter estimation code LALInference (which uses binary black hole waveforms). The bottom panels show time–frequency plots: each plot has a different scale as the signal is loudest in LIGO Livingston and hardly noticeable in Virgo. As the signal is so short, we don’t see the usual chirp of a binary coalescence clearly. Figure 1 of the GW190521 Discovery Paper.

After hearing that the initial checks were complete, I went to bed, little knowing the significance of what we had found. The initial estimates for the masses of a binary come from our search pipelines—specifically the pipelines that match signal templates to the data. At high masses, the search template bank doesn’t have many templates, so the best fitting template can be quite a way from the true value. It was only after completing a proper parameter estimation analysis that we get a good idea of the masses and their uncertainties. When these results came in we found that we potentially had something lying smack in the middle of the pair-instability mass gap. That was, if the signal were real.

While initial checks of the signal showed nothing suspicious, we always do more offline checks. For GW190521 there were a few questions that took some digging to understand.

First, the peak of the signal is around 60 Hz. This is also the mains frequency in the US, so there was concern that the signal was contaminated by noise caused by this (which would obviously be shocking). A variety of careful investigations were done subtracting out noise from the mains. In the end, it turns out that this makes negligible difference to the results, which is nice.

Second, there was concern over the shape of the signal. Our template-based search algorithms always look at how well the signal matches the template: if you get a really good match in one frequency range, but not another, then that’s an indicator that you have some random noise rather than a true signal. This consistency test is summarised in a statistic, which should be around 1 if all is OK, and larger if things don’t fit. For the PyCBC algorithm, the value for the Livingston data was about 3. Since the signal was loudest in Livingston, was this cause for alarm? One explanation could be that the template wasn’t a good fit because the templates used by the search don’t include the effects of spin precession. Hence, if you have a signal where spin precession is important, you would expect a bad fit. Checking the consistency with templates which included precession did give better consistency. However, the GstLAL algorithm also used templates without precession, and its consistency test looked fine. Therefore, it couldn’t just be precession. It seems that the key is that there are so few templates in the relevant area for PyCBC’s template bank (GstLAL had things better covered). Hence, it is hard to find a good fitting template. Adding the best fitting template from the GstLAL bank to the PyCBC search leads to it being picked out as the best template too, with a consistency check statistic of 1.7 (not perfect, but not suspicious). I think this highlights the importance of not limiting yourself to only finding what you expect: we need to include the potential for our searches to discover things outside of what we have discovered in the past.

Finally, there was the difference in significance reported by the different search algorithms. In addition to the template-based searches, we also have searches which look for more generic signals without templates [bonus note], instead using the consistency in the data from different detectors to spot signals. Famously, our non-template algorithm coherent WaveBurst (cWB) made the first detection of GW150914 (other algorithms weren’t up-and-running at the time). Usually, the template searches should do better as they know what they are looking for. This has mostly been the case so far. The exception was GW170729, our previously most massive and lowest significance detection. Generally, you expect searches to disagree more on quiet signals (not too much of an issue for GW190521), as then how they characterise the noise background is more important. We also expect the template searches to lose their advantage for very short signals, when there’s not much for a template to match, and when the coherence check used by cWB comes in especially handy. GW190521 is again found with greatest significance by cWB. In our final searches (using all the data from the first six months of the third observing run), cWB gives a false alarm rate of 1 per 4900 years (pretty darn good—at least a Jammie Wagon Wheel in biscuit terms), GstLAL gives 1 per 829 years (nice—a couple of Fruit Creme biscuits), and PyCBC gives 1 per 0.94 years (not at all exciting—an Iced Gem at best). Should we be suspicious of the difference? Perhaps cWB can pick up on something extra in the signal because actually the source isn’t a quasicircular binary [bonus note] as assumed by our templates? We know that the search templates are missing some features, like the effects of spin precession, and also higher order multipole moments. Seeing how our search algorithms cope finding simulated signals that include these extra bits of physics, we find that similar discrepancies between cWB and GstLAL happen around 8% of the time, while for cWB and PyCBC they happen about 3% of the time. That’s enough to make me go Hmm, but not enough to convince me that we’ve detected a completely new type of signal, one which doesn’t come from a quasicircular binary.

The conclusion from our analysis is that GW190521 is a good-looking gravitational wave signal. We are confident that it is a real detection, even though it is really short. However, we can’t be positive that the source is quasicircular binary. That’s the most likely explanation, and consistent with what we’ve seen, but potentially not the only explanation.

There are other sources for gravitational waves beyond quasicircular binaries. One of the best known would be a supernova explosion. GW190521 is certainly not one of these. For one thing, the signals are much longer and more complicated, and for another, we could really only detect a supernova within our own galaxy, and we probably would have noticed that happen. Another hypothesised search which could produce a nice, short bleep of a signal would be a cosmic string. Vibrations or ripples along a cosmic string can source gravitational waves, and while we don’t know if cosmic strings exist, we do have templates for what these signals should look like. Using these, we can compare how well the data are described by cosmic string signals compared to our quasiciruclar binary templates. We find Bayes factors of about $10^{30}$ in favour of the binary signals, so it’s probably not cosmic strings. Finally, you’ve perhaps noticed that I’ve been writing quasicircular [bonus note] a lot. Part of that is because it’s a cool word (25 points in Scrabble), but also because it’s possible that we have an eccentric binary. These are difficult to model, so we don’t have lots of good templates for them, but when you have a short signal, it is possible that eccentricity could be confused with spin precession. This would lead us to overestimating the distance and underestimating the masses. Initial studies do seem to show that an eccentric signal fits the data well (Romero-Shaw et al. 2020; Gayathri et al. 2020). An eccentric binary is the most probable alternative to a quasicircular binary, but it is pretty improbable. Since eccentricity is lost during inspiral, we would need something to have pumped the eccentricity, which is difficult for a binary so close to merger. I would bet my Oreos on the source being a quasicircular binary.

The source properties

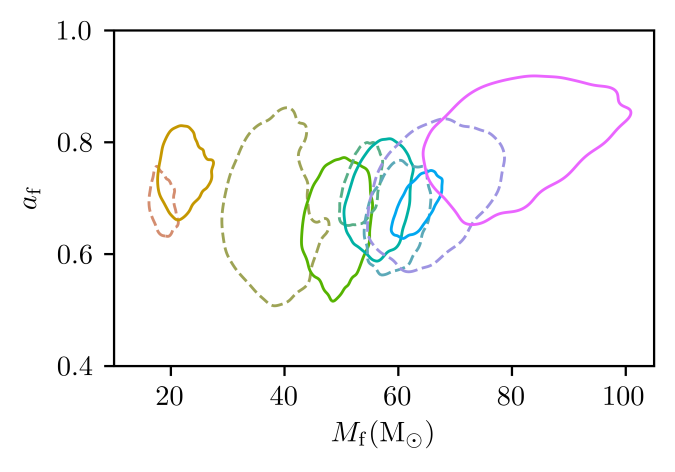
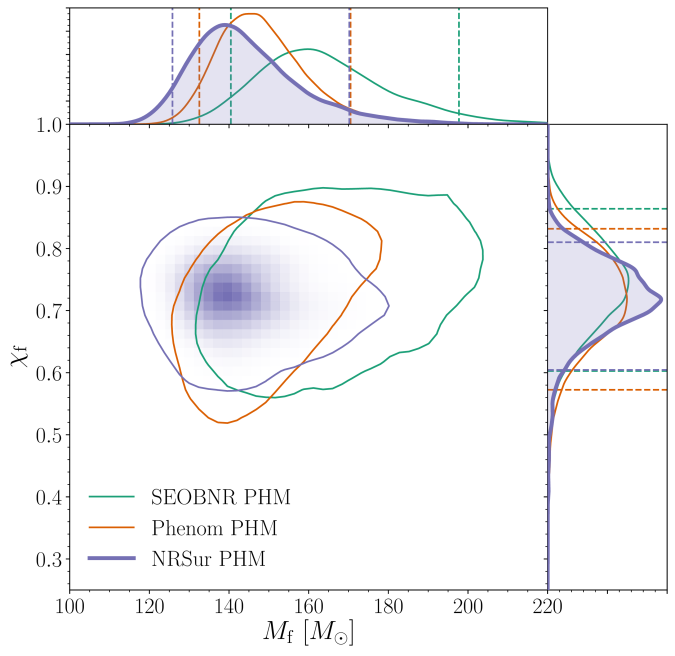
If we stick with the assumption of a quasicircular binary, what can we tell about the source? We have already covered the component masses of $m_1 = 85^{+21}_{-14} M_\odot$ and $m_2 = 66^{+17}_{-18} M_\odot$ , and that the merger remnant is $M_\mathrm{f} = 142^{+28}_{-16} M_\odot$ . The plot below shows the final mass as well as the spin, which is $\chi_\mathrm{f} = 0.72^{+0.09}_{-0.12}$ . For the black holes formed from the mergers of near equal mass binaries, you’d expect the final spin to be around $0.7$ .

Estimated mass $M_\mathrm{f}$ and spin $\chi_\mathrm{f}$ for the final black hole. We show results several different waveform models and use the numerical relativity surrogate (NRSur PHM) as our best results. The two-dimensional shows the 90% probability contour. The dotted lines in one-dimensional plots the symmetric 90% credible interval. The mass is safely above the conventional lower limit to be considered an intermediate-mass black hole. Figure 3 of the GW190521 Implications Paper.

We can also get an estimate of the final spin from the final part of the signal, the ringdown. This is where the black hole settles down to its final state, like me after 6 pm. What is neat about using the ringdown is that we don’t need to assume that the binary was quasicircular, as we only care about the black hole formed at the end. The downside is that we don’t get an estimate of the distance, so we only measure the redshifted final mass $(1+z)M_\mathrm{f}$ . Looking at the ringdown, we get lovely consistent results trying ringdown models at different start times and including different higher order multipole moments, and all agree with the analysis of the entire signal using the quasicircular templates.

Final black hole mass and spin measured from GW190521's ringdown

Estimated redshifted mass $(1+z)M_\mathrm{f}$ and spin $\chi_\mathrm{f}$ for the final black hole. We show results several different insprial–merger–ringdown waveform models, which we use for our standard analysis, as well as ringdown-only waveforms. They agree nicely. The two-dimensional shows the 90% probability contour. The dotted lines in one-dimensional plots the symmetric 90% credible interval. The mass is safely above the conventional lower limit to be considered an intermediate-mass black hole. Part of Figure 9 of the GW190521 Implications Paper.

Being able to measure the ringdown at all is an achievement. It’s only possible for loud signals from high mass systems. The consistency of the mass and spin estimates is not only a check of the quasicircular analysis. It is much more powerful than that. The ringdown measurements are a test of the black hole nature of the final object. All looks as expected so far. I really want to do this for louder signals in the future.

Returning to the initial binary, what can we say about the spins of the initial black holes? Not much, as it is difficult to extract information from such a short waveform.

The spin components aligned with the orbital angular momentum affect the transition from inspiral, and have a small influence on the final spin. We often quantify the aligned components of the spin in the mass-weighted effective inspiral spin parameter $\chi_\mathrm{eff}$ , which goes from $-1$ for both the spins being maximal and antialigned with the orbital angular momentum to $1$ for both spins being maximal and aligned with the orbital angular momentum. We find that $\chi_\mathrm{eff} = 0.08^{+0.27}_{-0.36}$ , consistent with no spin, spins antialigned with each other or in the orbital plane. The result is strongly influenced by the assumed prior, we’ve not learnt much from the signal.

The component of the spin in the orbital plane (perpendicular to the orbital angular momentum) control the amount of spin precession. We often quantify this using the effective precession spin parameter $\chi_\mathrm{p}$ , which goes from $0$ for no in-plane spin, to $1$ for maximal precession. Precession normally shows up in the modulation of the inspiral signal, so you wouldn’t expect to measure it well from a short signal. However, it can also influence to amplitude of the signal around merger, and we seem to get a bit of information here, which seems to prefer larger $\chi_\mathrm{p}$ . We find $\chi_\mathrm{p} = 0.68^{+0.28}_{-0.34}$ , but there’s support across the entire range.

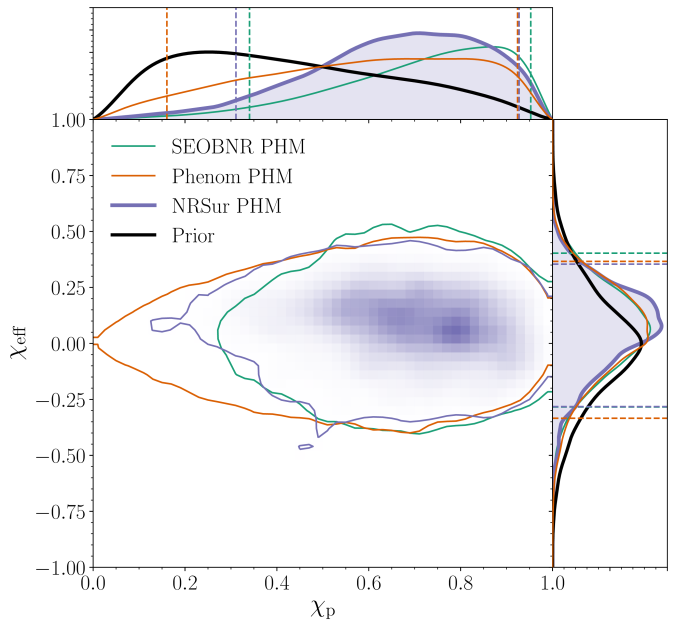
Effective inspiral spin and effective precession spin for GW190521

Estimated effective inspiral spin $\chi_\mathrm{eff}$ and effective precession spin $\chi_\mathrm{p}$ . We show results several different waveform models and use the numerical relativity surrogate (NRSur PHM) as our best results. The two-dimensional shows the 90% probability contour. The dotted lines in one-dimensional plots the symmetric 90% credible interval. We also show the prior distributions in the one-dimensional plots. Part of Figure 1 of the GW190521 Implications Paper.

Looking at the spins overall, the lack of aligned spin plus the support for in-plane spins means that we prefer misaligned spins. You wouldn’t expect this for two stars which have lived their lives together as a binary, but it wouldn’t be implausible for a dynamically formed binary. A dynamical formation seems plausible to me, but since the spin measurements aren’t too concrete, we can’t really rule too much out [bonus note].

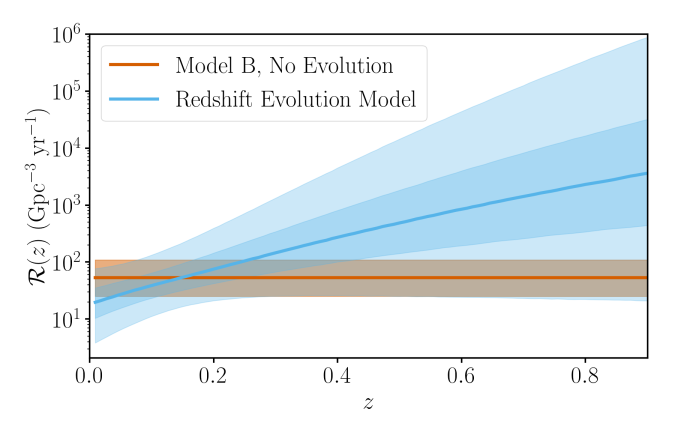
Finally, let’s take a look at the distance to the source. Our analysis gives a luminosity distance of $D_\mathrm{L} 5.3^{+2.4}_{-2.6}~\mathrm{Gpc}$ . This makes the source a good contender for the most distant gravitational wave source ever found [bonus note]. It’s actually far enough, that we might want to reconsider our standard approximation that sources are uniformly distributed like $D_\mathrm{L}^2$ . This would be OK if sources were uniformly distributed in a non-evolving Universe, but sadly we don’t live in such a thing, and we have to take into account the expansion of the Universe, and the evolution of the galaxies and stars within it. We’ll come back to look at this when we present our catalogue of detections from the first part of the third observing run.

The astrophysics

Exploring the upper mass gap

The location of the upper mass gap is pretty well determined. There are a variety of uncertainties in the input physics, such as the nuclear reaction rate for burning carbon into oxygen, the treatment of convection inside stars or if stars rapidly rotate which can alter the cut-off. No-one has tried varying all these together, but individually you can’t get above about $55 M_\odot$ for your black hole. Allowing for new types of particles (like axions, one of the candidates for dark matter, and possibly the explanation for why teenage boys can smell terrible) can potentially increase the limit to above $70 M_\odot$ , but that is extremely speculative (I’d love it if it were true). Sticking to known physics, at face value, it is hard to explain the mass of the primary black hole from our understanding of how stars evolve.

There are potentially ways around the mass gap with help from a star’s environment:

Super efficient accretion from a companion star can grow black holes into the mass gap. Then you wouldn’t expect the total mass of the binary to over about $100 M_\odot$ , so we’d need to swap out partners in this case.
The pair instability originates in the helium core of a star. If we can find a way to grow the envelope of the star, while keeping the core below the threshold for the instability to set in, then the whole thing could collapse down to a mass gap black hole. This could potentially happen if two stars collide after one has already formed its helium core. The other gets disrupted and swells the envelope. This might be expected in stellar clusters. Similarly, a couple of recent papers (Farrell et al. 2020; Kinugawa, Nakamura & Nakano 2020) have also suggested that the first generation of stars, which have few elements other than hydrogen or helium, could also collapse down to black holes in this mass range. The idea here is that these stars lose much less of their envelopes due to stellar winds, so you can end up with what we would otherwise consider an oversized envelope around a core below the pair instability threshold
We could have two black holes merge to form a bigger one, and then have the remnant go on to form a new binary. You would need a dense environment for this, somewhere like a globular cluster where it’s easy to find new partners. Ideally, somewhere with a large escape velocity, perhaps a nuclear star cluster, which has a high escape velocity so that it is more difficult for the remnant black hole to get kicked out at any point: gravitational waves give a recoil kick, and close encounters with other objects can also lead to the initial binary getting a kick.
Especially good for growing black holes may be if they are embedded in the accretion disc around a supermassive black hole. Then these disc black holes can merge with each other whilst being unlikely to escape the environment. Additionally, they can swallow lots of gas from the surrounding disc to help them grow big and strong.

There is also the potential that we don’t have a black hole formed from stellar collapse, but instead a primordial black hole formed from dense regions in the early Universe. These primordial black holes are a another candidate for dark matter. I like that there are two options for potential dark matter-related formation channels. It’s good to have options.

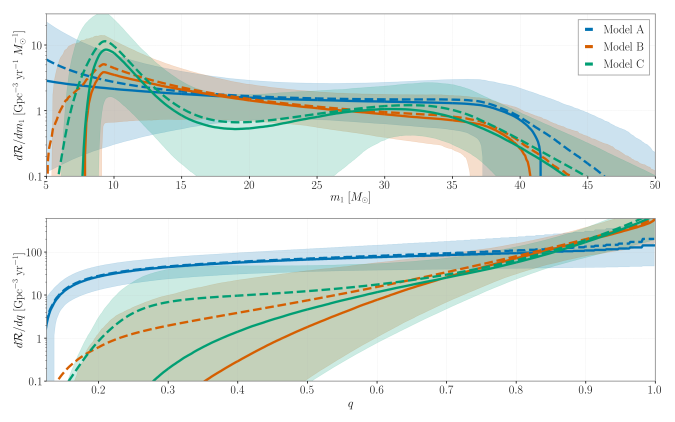
The difficulty with all of these alternative formation channels is matching the observed rate for GW190521-like systems. It’s not enough for a proposed channel to be able to explain the system’s properties, it also needs to make enough of them for us to have come across one. From our data, we infer that GW190521-like systems have a merger rate density of $0.13^{+0.30}_{-0.11}~\mathrm{Gpc^{-3}\,yr^{-1}}$ . Predicted rates for the various formation mechanisms discussed above can be rather uncertain (kind of like how the exact value of a small bag full of Bitcoin is uncertain), so I would like to see more work on this, before picking a most plausible option.

Hierarchical mergers

We did do some quantitative analysis for the case of hierarchical mergers of black holes, following the framework outlined in Kimball et al. (2020). This simultaneously fits the mass and spin distribution for the first generation (1g) of black holes formed from stars, and a fraction of hierarchical mergers involving second generation (2g) merger remnants. To calibrate the number of hierarchical mergers, we use globular cluster simulations.

Using our base model, where the 1g+1g population is basically the Model C we used to describe our detections from the first two observing runs, we find that the odds are in favour of GW190521 being a 1g+1g merger. Hierarchical mergers are so rare, that it’s actually more probable that we squish down the inferred masses and have something from the tail of the 1g population.

The rate of hierarchical mergers, however, is very sensitive to the distribution of spins of 1g black holes. Larger spins give bigger kicks (even a spin of 0.1 is enough to mean remnants are hardly ever retained in typical globular clusters). If we add into the mix a fraction of 1g+1g binaries which have 0 spin (motivated by recent simulations), we improve the odds to be roughly even 1g+1g vs 1g+2g, and less common for 2g+2g. Given that we are not taken into account that only a fraction of binaries would be in clusters, which would reduce the odds of a hierarchical merger considerably, this isn’t quite enough to convince me.

However, what if we were to turn up the mass of the cluster? For our globular cluster model, we used $5\times 10^5 M_\odot$ , what if we tried $10^8 M_\odot$ , more like you would expect for a nuclear star cluster? We shouldn’t really be doing this, as our model is calibrated against globular cluster simulations, and nuclear star clusters have different dynamics, but we can use our results as illustrative. In this case, we find odds of about 1000:1 in favour of hierarchical mergers. This suggests that this option may be a promising one to follow, but we must moderate our results remembering that only a fraction of binaries would form in these dense environments.

The analysis is done using only our first 10 detected binary black hole from our first two observing runs plus GW190521. GW190521 is not the most representative of the third observing run detections (hence why it gets special papers™), so it is not exactly fair to stick it in to the mix to infer the population parameters. We’ll need to redo this analysis when we have the full results of the run to update the results. Having more binaries in the analysis should allow us to more precisely measure the population parameters, so we will be more confident in our results.

The surprise

After all our investigations, we thought we had examined every aspect of GW190521. However, there’s always one more thing. As we were finishing up the paper, a potential electromagnetic counterpart was announced.

Electromagnetic counterparts are not expected when two black holes merge—black holes are indeed black—however, material around the binary could produce light.

The counterpart was found by the Zwicky Transient Factory. They targeted active galactic nuclei to look for counterparts. These are the bright cores of galaxies where the supermassive black hole is feeding off a surrounding disc. In this case, they hypothesis that the binary had some gas orbiting around it, and when the binary merged, the gravitational wave recoil kick sent the remnant black hole and its orbiting material into the disc of the supermassive black hole. As the orbiting material crashes into the disc it will emit light. Then, once it is blasted away, material from the disc accreting onto the remnant black hole will also emit light. This seems to fit with what was observed, with the later powering the observed emission.

What I think is exciting about this proposal is that active galactic nuclei are one of the channels predicted to produce binaries as massive as GW190521! Therefore, things seem to line up nicely.

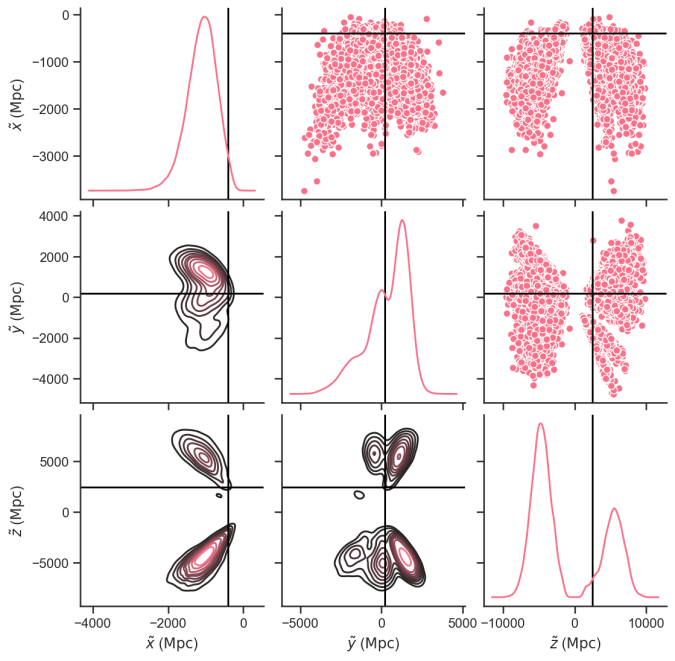
Three dimensional localisation and active galactic nucleus location

The three dimensional localisation for GW190521. The lines indicate the position of the claimed electromagnetic counterpart from around an active galactic nucleus. This location lies at the 70% credible level. Credit: Will Farr

What I think is less certain is if the counterpart is really associated with our gravitational wave source. The observing team estimate that the probability of a chance association is small. However, there is a lot of uncertainty in how active galactic nuclei can flare. The good news is that the remnant black hole may continue to orbit and hit the disc again, leading to another flare. The bad news is that the uncertainty on when this happens is many years, so we don’t know when to look.

Follow-up analyses by Ashton et al. (2020) and Palmese et al. (2021) cast the association as more uncertain. It is difficult to be confident of an association when the localization volume is so large. If we knew that this type of flare had to look exactly like the observed emission, that would help, but we can’t be that certain yet.

Overall, I think we need to observe another similar association before we can be certain what’s going on. I really hope this candidate counterpart encourages people to follow up more binary black holes to look for emission. The unexpected discoveries are often the most rewarding.

The papers

The GW190521 Discovery Paper

Title: GW190521: A binary black hole merger with a total mass of 150 solar masses
Journal: Physical Review Letters; 125(10):101102(17)
arXiv: 2009.01075 [gr-qc]
Read this if: You want to understand the detection of GW190521

This is the paper announcing the gravitational wave detection. It follows our now standard pattern for a detection paper of discussing our instruments and data quality; our detection algorithms and the statistical significance of the search; the inferred properties of the source, and a bit of testing gravity; a check of the reconstruction of the waveform, and then a nice summary looking forward to more discoveries to come.

What is a little different for this paper is that because the signal is so short, we have had to be extra careful in our checks of the detectors’ statuses, the reliability of our detection algorithms, and the assumptions that go into estimating the source properties. If you are sceptical of being able to detect such short signals, I recommend checking out the Supplemental Material for a summary of some of the tests we did.

The GW190521 Implications Paper

Title: Properties and astrophysical implications of the 150 solar mass binary black hole merger GW190521
Journal: Astrophysical Journal Letters; 900(1):L13(27)
arXiv: 2009.01190 [astro-ph.HE]
Read this if: You want to understand the implications for fundamental physics and astrophysics of the discovery

In this paper we explore the properties of GW190521. We check the robustness of the inferred source properties. For such a short signal, our usual assumption that we have a quasicircular binary is probably the most sensible thing to do, but we can’t be certain, and if this assumption is wrong, then we will have got the properties wrong. Astronomy is hard sometimes. Assuming that our estimates of the properties are correct, we look at potential formation mechanisms. We don’t come to any firm conclusions, but sketch out some of the possibilities. We also look at tests of the black hole nature of the final object in a bit more detail. A few wibbles can sure cause a lot of excitement.

Science summary: GW190521: The most massive black hole collision observed to date
Data release: Gravitational Wave Open Science Center; Parameter estimation results
Rating: 🍰🐋📏🏆

Bonus notes

Squeezing

Please hug responsibly.

Minimum black hole mass

The uncertainty in when gravity will take over and squish things down to a black hole is set by the stiffness of neutron star matter. Neutron stars are the densest matter can be, this is the stiffest form of matter, the one most resistant to being crushed down into a black hole. The amount of weight neutron star matter can support is uncertain, so we don’t quite know their maximum mass yet. This made the discovery of GW190814 particularly intriguing. This gravitational wave came from a binary where the less massive component was about $2.6 M_\odot$ , exactly in the range where we’d expect the transition between neutron stars and black holes. We can’t tell for certain which it is, but I’ve bet my M&Ms on a black hole.

It’s potentially possible that there are black holes smaller than the maximum neutron star mass which didn’t form from collapsing stars. These are primordial black holes, which formed from overdense regions in the early universe. We don’t know for certain if they do exist, but we are looking.

Positrons

Positrons are antielectrons, the antimatter equivalent of electrons. This means that they share identical properties to electrons except that they have opposite charge. Electrons things that the glass is half-empty, positrons think it is half-full. Neutrinos think that the glass is twice as big as it needs to be, but so long as we have a well-mixed cocktail, who cares?

Burst searches

In the jargon of LIGO and Virgo, we refer to the non-template detection algorithms as Burst searches, as they are good at spotting bursts of gravitational waves. Burst is not a terribly useful description if you’ve not met it before, so we generally try to avoid this in our papers. A common description is an unmodelled search, to distinguish from the template-based searches which use model waveforms as input. However, it’s not really true that the Burst searches don’t make modelling assumptions about the signal. For example, the cWB algorithm used to look for binaries assumes that the frequency will increase with time (as you would expect for an inspiralling binary). To avoid this, we’ve sometimes describes the search algorithm as weakly modelled, but that’s perhaps no clearer than Burst. For this post, I’ll stick to non-template as a description.

Quasicircular

When talking about the orbits of binaries, we might be interested in their eccentricity. Eccentricity is a key tracer of how the binary formed. As binaries emit gravitational waves, they quickly lose their eccentricity, so in general we don’t expect there to be significant eccentricity for the binaries detected by LIGO and Virgo.

An orbit with zero eccentricity should be circular. However, since we have a binary emitting gravitational waves the orbit will be shrinking. As we have an inspiral, if you were to trace out the orbit, it would not be a circle, even though we would describe it as having zero eccentricity. This is particularly noticeable at the end of the inspiral, when we get close to the two objects plunging together. Hence, we describe orbits as quasicircular, which I think sounds rather cute.

The simulation above shows the orbit of an inspiral. Here the spins of the black holes also lead to the precession of the orbit, making it a bit more complicated than you might expect for a something described as circular, but, of course, not at all unexpected for something with a cool name like quasicircular. I also really like how this visualisation shows the event horizons of the two black holes merging.

Spin Bayes factors

To try to quantify the support for spin, we quote two Bayes factors. The first is for spin verses no spin. There we find a Bayes factor of about 8.3 in favour of there being spin. That’s not something you’d want to bet against, but for comparison, for GW190412 we found that is it over 400, and for GW151226 it is over a million. I’d expect any statement on spins for GW190521 will depend upon your prior assumptions. The second Bayes factor is in favour of measurable precession. This is not the same as comparing the Bayes factor between perfectly aligned spins (when there would be no precession) and generic, isotropically distributed spins. Instead we are comparing the scenario where we can measure in-plane spins verses the case where there are isotropically distributed but the in-plane spins don’t have any discernible consequences. Here we find a Bayes factor of 11.5 in favour of measurable precession. This makes sense as we do have some information on $\chi_\mathrm{p}$ , and would expect an even Bayes factor of 1 if we only got the prior back. It seems we have gained some information about the spins from the signal.

For more on Bayes factors, I would suggest reading Zevin et al. (2020). In particular, this explains why it can make sense here that the Bayes factor for measurable precession is larger than the Bayes factor for there being spin. At first, it might appear odd that we can be more definite that there is precession than any spin at all. However, this is because in comparing spin verses no spin we are hit by the Occam factor—we are adding extra parameters to our model, and we are penalised for this. If the effects of spins are small, so that they are not worth including, we would expect no-spin to win. When looking at the measurability of precession, we have set up the comparison so that there is no Occam factor. We can only win, if waveforms with precession clearly fit the data better, or break even if they make no difference.

Economically large

To put a luminosity distance of $5.3~\mathrm{Gpc}$ in context, if you put $1 in a jar ever two weeks over the duration the gravitational wave signal was travelling from its source to us (7.1 billion years, about 1.5 times the age of the Sun), you would end up with about a net worth only 7% less than Jeff Bezos (currently $199.3 billion).

The O2 Catalogue—It goes up to 11

December 7, 2018January 26, 2020 / CPLB / Leave a comment

The full results of our second advanced-detector observing run (O2) have now been released—we’re pleased to announce four new gravitational wave signals: GW170729, GW170809, GW170818 and GW170823 [bonus note]. These latest observations are all of binary black hole systems. Together, they bring our total to 10 observations of binary black holes, and 1 of a binary neutron star. With more frequent detections on the horizon with our third observing run due to start early 2019, the era of gravitational wave astronomy is truly here.

The population of black holes and neutron stars observed with gravitational waves and with electromagnetic astronomy. You can play with an interactive version of this plot online.

The new detections are largely consistent with our previous findings. GW170809, GW170818 and GW170823 are all similar to our first detection GW150914. Their black holes have masses around 20 to 40 times the mass of our Sun. I would lump GW170104 and GW170814 into this class too. Although there were models that predicted black holes of these masses, we weren’t sure they existed until our gravitational wave observations. The family of black holes continues out of this range. GW151012, GW151226 and GW170608 fall on the lower mass side. These overlap with the population of black holes previously observed in X-ray binaries. Lower mass systems can’t be detected as far away, so we find fewer of these. On the higher end we have GW170729 [bonus note]. Its source is made up of black holes with masses $50.2^{+16.2}_{-10.2} M_\odot$ and $34.0^{+9.1}_{-10.1} M_\odot$ (where $M_\odot$ is the mass of our Sun). The larger black hole is a contender for the most massive black hole we’ve found in a binary (the other probable contender is GW170823’s source, which has a $39.5^{+11.2}_{-6.7} M_\odot$ black hole). We have a big happy family of black holes!

Of the new detections, GW170729, GW170809 and GW170818 were both observed by the Virgo detector as well as the two LIGO detectors. Virgo joined O2 for an exciting August [bonus note], and we decided that the data at the time of GW170729 were good enough to use too. Unfortunately, Virgo wasn’t observing at the time of GW170823. GW170729 and GW170809 are very quiet in Virgo, you can’t confidently say there is a signal there [bonus note]. However, GW170818 is a clear detection like GW170814. Well done Virgo!

Using the collection of results, we can start understand the physics of these binary systems. We will be summarising our findings in a series of papers. A huge amount of work went into these.

The papers

The O2 Catalogue Paper

Title: GWTC-1: A gravitational-wave transient catalog of compact binary mergers observed by LIGO and Virgo during the first and second observing runs
arXiv: 1811.12907 [astro-ph.HE]
Data: Catalogue; Parameter estimation results
Journal: Physical Review X; 9(3):031040(49); 2019
LIGO science summary: GWTC-1: A new catalog of gravitational-wave detections

The paper summarises all our observations of binaries to date. It covers our first and second observing runs (O1 and O2). This is the paper to start with if you want any information. It contains estimates of parameters for all our sources, including updates for previous events. It also contains merger rate estimates for binary neutron stars and binary black holes, and an upper limit for neutron star–black hole binaries. We’re still missing a neutron star–black hole detection to complete the set.

More details: The O2 Catalogue Paper

The O2 Populations Paper

Title: Binary black hole population properties inferred from the first and second observing runs of Advanced LIGO and Advanced Virgo
arXiv: 1811.12940 [astro-ph.HE]
Journal: Astrophysical Journal Letters; 882(2):L24(30); 2019
Data: Population inference results
LIGO science summary: Binary black hole properties inferred from O1 and O2

Using our set of ten binary black holes, we can start to make some statistical statements about the population: the distribution of masses, the distribution of spins, the distribution of mergers over cosmic time. With only ten observations, we still have a lot of uncertainty, and can’t make too many definite statements. However, if you were wondering why we don’t see any more black holes more massive than GW170729, even though we can see these out to significant distances, so are we. We infer that almost all stellar-mass black holes have masses less than $45 M_\odot$ .

More details: The O2 Populations Paper

The O2 Catalogue Paper

Synopsis: O2 Catalogue Paper
Read this if: You want the most up-to-date gravitational results
Favourite part: It’s out! We can tell everyone about our FOUR new detections

This is a BIG paper. It covers our first two observing runs and our main searches for coalescing stellar mass binaries. There will be separate papers going into more detail on searches for other gravitational wave signals.

The instruments

Gravitational wave detectors are complicated machines. You don’t just take them out of the box and press go. We’ll be slowly improving the sensitivity of our detectors as we commission them over the next few years. O2 marks the best sensitivity achieved to date. The paper gives a brief overview of the detector configurations in O2 for both LIGO detectors, which did differ, and Virgo.

During O2, we realised that one source of noise was beam jitter, disturbances in the shape of the laser beam. This was particularly notable in Hanford, where there was a spot on the one of the optics. Fortunately, we are able to measure the effects of this, and hence subtract out this noise. This has now been done for the whole of O2. It makes a big difference! Derek Davis and TJ Massinger won the first LIGO Laboratory Award for Excellence in Detector Characterization and Calibration™ for implementing this noise subtraction scheme (the award citation almost spilled the beans on our new detections). I’m happy that GW170104 now has an increased signal-to-noise ratio, which means smaller uncertainties on its parameters.

The searches

We use three search algorithms in this paper. We have two matched-filter searches (GstLAL and PyCBC). These compare a bank of templates to the data to look for matches. We also use coherent WaveBurst (cWB), which is a search for generic short signals, but here has been tuned to find the characteristic chirp of a binary. Since cWB is more flexible in the signals it can find, it’s slightly less sensitive than the matched-filter searches, but it gives us confidence that we’re not missing things.

The two matched-filter searches both identify all 11 signals with the exception of GW170818, which is only found by GstLAL. This is because PyCBC only flags signals above a threshold in each detector. We’re confident it’s real though, as it is seen in all three detectors, albeit below PyCBC’s threshold in Hanford and Virgo. (PyCBC only looked at signals found in coincident Livingston and Hanford in O2, I suspect they would have found it if they were looking at all three detectors, as that would have let them lower their threshold).

The search pipelines try to distinguish between signal-like features in the data and noise fluctuations. Having multiple detectors is a big help here, although we still need to be careful in checking for correlated noise sources. The background of noise falls off quickly, so there’s a rapid transition between almost-certainly noise to almost-certainly signal. Most of the signals are off the charts in terms of significance, with GW170818, GW151012 and GW170729 being the least significant. GW170729 is found with best significance by cWB, that gives reports a false alarm rate of $1/(50~\mathrm{yr})$ .

Cumulative histogram of results from GstLAL (top left), PyCBC (top right) and cWB (bottom). The expected background is shown as the dashed line and the shaded regions give Poisson uncertainties. The search results are shown as the solid red line and named gravitational-wave detections are shown as blue dots. More significant results are further to the right of the plot. Fig. 2 and Fig. 3 of the O2 Catalogue Paper.

The false alarm rate indicates how often you would expect to find something at least as signal like if you were to analyse a stretch of data with the same statistical properties as the data considered, assuming that they is only noise in the data. The false alarm rate does not fold in the probability that there are real gravitational waves occurring at some average rate. Therefore, we need to do an extra layer of inference to work out the probability that something flagged by a search pipeline is a real signal versus is noise.

The results of this calculation is given in Table IV. GW170729 has a 94% probability of being real using the cWB results, 98% using the GstLAL results, but only 52% according to PyCBC. Therefore, if you’re feeling bold, you might, say, only wager the entire economy of the UK on it being real.

We also list the most marginal triggers. These all have probabilities way below being 50% of being real: if you were to add them all up you wouldn’t get a total of 1 real event. (In my professional opinion, they are garbage). However, if you want to check for what we might have missed, these may be a place to start. Some of these can be explained away as instrumental noise, say scattered light. Others show no obvious signs of disturbance, so are probably just some noise fluctuation.