Advanced LIGO’s first observing run (O1) got off to an auspicious start with the detection of GW150914 (The Event to its friends). O1 was originally planned to be three months long (September to December), but after the first discovery, there were discussions about extending the run. No major upgrades to the detectors were going to be done over the holidays anyway, so it was decided that we might as well leave them running until January.
By the time the Christmas holidays came around, I was looking forward to some time off. And, of course, lots of good food and the Doctor Who Christmas Special. The work on the first detection had been exhausting, and the Collaboration reached the collective decision that we should all take some time off [bonus note]. Not a creature was stirring, not even a mouse.
On Boxing Day, there was a sudden flurry of emails. This could only mean one thing. We had another detection! Merry GW151226 [bonus note]!

I assume someone left out milk and cookies at the observatories. A not too subtle hint from Nutsinee Kijbunchoo’s comic in the LIGO Magazine.
I will always be amazed how lucky we were detecting GW150914. This could have been easily missed if we were just a little later starting observing. If that had happened, we might not have considered extended O1, and would have missed GW151226 too!
GW151226 is another signal from a binary black hole coalescence. This wasn’t too surprising at the time, as we had estimated such signals should be pretty common. It did, however, cause a slight wrinkle in discussions of what to do in the papers about the discovery of GW150914. Should we mention that we had another potential candidate? Should we wait until we had analysed the whole of O1 fully? Should we pack it all in and have another slice of cake? In the end we decided that we shouldn’t delay the first announcement, and we definitely shouldn’t rush the analysis of the full data set. Therefore, we went ahead with the original plan of just writing about the first month of observations and giving slightly awkward answers, mumbling about still having data to analyse, when asked if we had seen anything else [bonus note]. I’m not sure how many people outside the Collaboration suspected.
The science
What have we learnt from analysing GW151226, and what have we learnt from the whole of O1? We’ve split our results into two papers.
0. The Boxing Day Discovery Paper
Title: GW151226: Observation of gravitational waves from a 22-solar-mass binary black hole
arXiv: 1606.04855 [gr-qc]
Journal: Physical Review Letters; 116(24):241103(14)
LIGO science summary: GW151226: Observation of gravitational waves from a 22 solar-mass binary black hole (by Hannah Middleton and Carl-Johan Haster)
This paper presents the discovery of GW151226 and some of the key information about it. GW151226 is not as loud as GW150914, you can’t spot it by eye in the data, but it still stands out in our search. This is a clear detection! It is another binary black hole system, but it is a lower mass system than GW150914 (hence the paper’s title—it’s a shame they couldn’t put in the error bars though).
This paper summarises the highlights of the discovery, so below, I’ll explain these without going into too much technical detail.
More details: The Boxing Day Discovery Paper summary
1. The O1 Binary Black Hole Paper
Title: Binary black hole mergers in the first Advanced LIGO observing run
arXiv: 1606.04856 [gr-qc]
Journal: Physical Review X; 6(4):041015(36)
Posterior samples: Release v1.0
This paper brings together (almost) everything we’ve learnt about binary black holes from O1. It discusses GW150915, LVT151012 and GW151226, and what we are starting to piece together about stellar-mass binary black holes from this small family of gravitational-wave events.
For the announcement of GW150914, we put together 12 companion papers to go out with the detection announcement. This paper takes on that role. It is Robin, Dr Watson, Hermione and Samwise Gamgee combined. There’s a lot of delicious science packed into this paper (searches, parameter estimation, tests of general relativity, merger rate estimation, and astrophysical implications). In my summary below, I’ll delve into what we have done and what our results mean.
The results of this paper have now largely been updated in the O2 Catalogue Paper.
More details: The O1 Binary Black Hole Paper summary
If you are interested in our science results, you can find data releases accompanying the events at the LIGO Open Science Center. These pages also include some wonderful tutorials to play with.
The Boxing Day Discovery Paper
Synopsis: Boxing Day Discovery Paper
Read this if: You are excited about the discovery of GW151226
Favourite part: We’ve done it again!
The signal
GW151226 is not as loud as GW150914, you can’t spot it by eye in the data. Therefore, this paper spends a little more time than GW150914’s Discovery Paper talking about the ingredients for our searches.
GW151226 was found by two pipelines which specifically look for compact binary coalescences: the inspiral and merger of neutron stars or black holes. We have templates for what we think these signals should look like, and we filter the data against a large bank of these to see what matches [bonus note].
For the search to work, we do need accurate templates. Figuring out what the waveforms for binary black coalescence should look like is a difficult job, and has taken almost as long as figuring out how to build the detectors!
The signal arrived at Earth 03:38:53 GMT on 26 December 2015 and was first identified by a search pipeline within 70 seconds. We didn’t have a rapid templated search online at the time of GW150914, but decided it would be a good idea afterwards. This allowed us to send out an alert to our astronomer partners so they could look for any counterparts (I don’t think any have been found [bonus note]).
The unmodelled searches (those which don’t use templates, but just coherent signals in both detectors) which first found GW150914 didn’t find GW151226. This isn’t too surprising, as they are less sensitive. You can think of the templated searches as looking for Wally (or Waldo if you’re North American), using the knowledge that he’s wearing glasses, and a red and white stripped bobble hat, but the unmodelled searches are looking for him just knowing that he’s the person that’s on on every page.
GW151226 is the second most significant event in the search for binary black holes after The Event. Its significance is not quite off the charts, but is great enough that we have a hard time calculating exactly how significant it is. Our two search pipelines give estimates of the p-value (the probability you’d see something at least this signal-like if you only had noise in your detectors) of and
, which are pretty good!
The source
To figure out the properties of the source, we ran our parameter-estimation analysis.
GW151226 comes from a black hole binary with masses of and
[bonus note], where
is the mass of our Sun (about 330,000 times the mass of the Earth). The error bars indicate our 90% probability ranges on the parameters. These black holes are less massive than the source of GW150914 (the more massive black hole is similar to the less massive black hole of LVT151012). However, the masses are still above what we believe is the maximum possible mass of a neutron star (around
). The masses are similar to those observed for black holes in X-ray binaries, so perhaps these black holes are all part of the same extended family.
A plot showing the probability distributions for the masses is shown below. It makes me happy. Since GW151226 is lower mass than GW150914, we see more of the inspiral, the portion of the signal where the two black holes are spiralling towards each other. This means that we measure the chirp mass, a particular combination of the two masses really well. It is this which gives the lovely banana shape to the distribution. Even though I don’t really like bananas, it’s satisfying to see this behaviour as this is what we have been expecting too see!
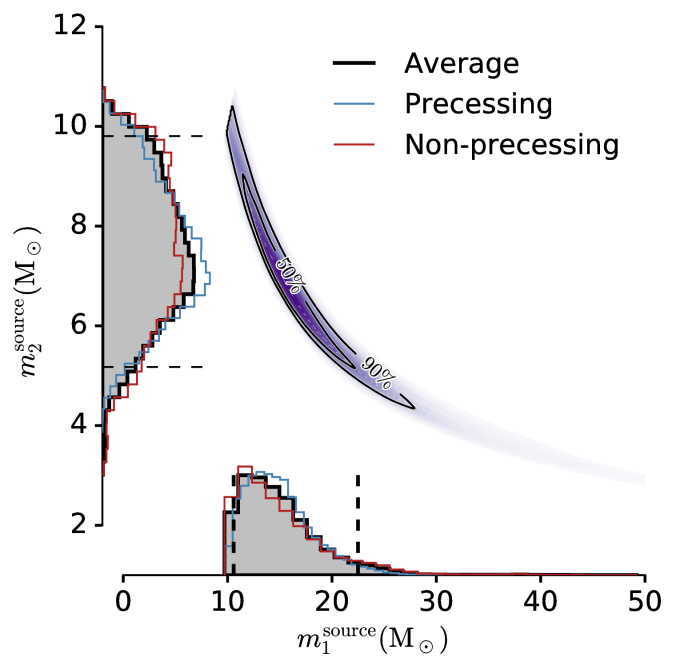
Estimated masses for the two black holes in the binary of the Boxing Day Event. The dotted lines mark the edge of our 90% probability intervals. The different coloured curves show different models: they agree which again made me happy! The two-dimensional distribution follows a curve of constant chirp mass. The sharp cut-off at the top-left is because is defined to be bigger than
. Figure 3 of The Boxing Day Discovery Paper.
The two black holes merge to form a final black hole of [bonus note].
If you add up the initial binary masses and compare this to the final mass, you’ll notice that something is missing. Across the entire coalescence, gravitational waves carry away of energy (where
is the speed of light, which is used to convert masses to energies). This isn’t quite as impressive as the energy of GW150914, but it would take the Sun 1000 times the age of the Universe to output that much energy.
The mass measurements from GW151226 are cool, but what’re really exciting are the spin measurements. Spin, as you might guess, is a measure of how much angular momentum a black hole has. We define it to go from zero (not spinning) to one (spinning as much as is possible). A black hole is fully described by its mass and spin. The black hole masses are most important in defining what a gravitational wave looks like, but the imprint of spin is more subtle. Therefore its more difficult to get a good measurement of the spins than the masses.
For GW150915 and LVT151012, we get a little bit of information on the spins. We can conclude that the spins are probably not large, or at least they are not large and aligned with the orbit of the binary. However, we can’t say for certain that we’ve seen any evidence that the black holes are spinning. For GW151226, al least one of the black holes (although we can’t say which) has to be spinning [bonus note].
The plot below shows the probability distribution for the two spins of the binary black holes. This shows the both the magnitude of the spin and the direction that of the spin (if the tilt is zero the black hole and the binary’s orbit both go around in the same way). You can see we can’t say much about the spin of the lower mass black hole, but we have a good idea about the spin of the more massive black hole (the more extreme the mass ratio, the less important the spin of lower mass black is, making it more difficult to measure). Hopefully we’ll learn more about spins in future detections as these could tell us something about how these black holes formed.
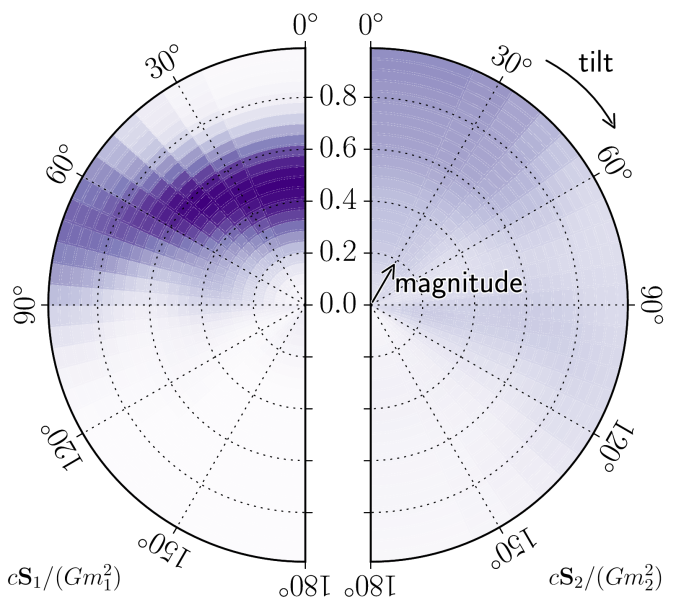
Estimated orientation and magnitude of the two component spins. Calculated with our precessing waveform model. The distribution for the more massive black hole is on the left, and for the smaller black hole on the right. Part of Figure 4 of The Boxing Day Discovery Paper.
There’s still a lot to learn about binary black holes, and future detections will help with this. More information about what we can squeeze out of our current results are given in the O1 Binary Black Hole Paper.
The O1 Binary Black Hole Paper
Synopsis: O1 Binary Black Hole Paper
Read this if: You want to know everything we’ve learnt about binary black holes
Favourite part: The awesome table of parameters at the end
This paper contains too much science to tackle all at once, so I’ve split it up into more bite-sized pieces, roughly following the flow of the paper. First we discuss how we find signals. Then we discuss the parameters inferred from the signals. This is done assuming that general relativity is correct, so we check for any deviations from predictions in the next section. After that, we consider the rate of mergers and what we expect for the population of binary black holes from our detections. Finally, we discuss our results in the context of wider astrophysics.
Searches
Looking for signals hidden amongst the data is the first thing to do. This paper only talks about the template search for binary black holes: other search results (including the results for binaries including neutron stars) we will reported elsewhere.
The binary black hole search was previously described in the Compact Binary Coalescence Paper. We have two pipelines which look for binary black holes using templates: PyCBC and GstLAL. These look for signals which are found in both detectors (within 15 ms of each other) which match waveforms in the template bank. A few specifics of these have been tweaked since the start of O1, but these don’t really change any of the results. An overview of the details for both pipelines are given in Appendix A of the paper.
The big difference from Compact Binary Coalescence Paper is the data. We are now analysing the whole of O1, and we are using an improved version of the calibration (although this really doesn’t affect the search). Search results are given in Section II. We have one new detection: GW151226.
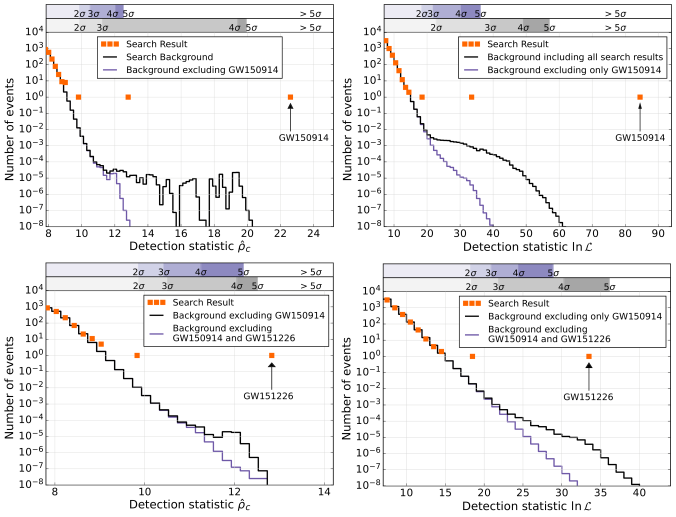
Search results for PyCBC (left) and GstLAL (right). The histograms show the number of candidate events (orange squares) compare to the background. The further an orange square is to the right of the lines, the more significant it is. Different backgrounds are shown including and excluding GW150914 (top row) and GW151226 (bottom row). Figure 3 from the O1 Binary Black Hole Paper.
The plots above show the search results. Candidates are ranked by a detection statistic (a signal-to-noise ratio modified by a self-consistency check for PyCBC, and a ratio of likelihood for the signal and noise hypotheses
for GstLAL). A larger detection statistic means something is more signal-like and we assess the significance by comparing with the background of noise events. The further above the background curve an event is, the more significant it is. We have three events that stand out.
Number 1 is GW150914. Its significance has increased a little from the first analysis, as we can now compare it against more background data. If we accept that GW150914 is real, we should remove it from the estimation of the background: this gives us the purple background in the top row, and the black curve in the bottom row.
GW151226 is the second event. It clearly stands out when zooming in for the second row of plots. Identifying GW150914 as a signal greatly improves GW151226’s significance.
The final event is LVT151012. Its significance hasn’t changed much since the initial analysis, and is still below our threshold for detection. I’m rather fond of it, as I do love an underdog.
Parameter estimation
To figure out the properties of all three events, we do parameter estimation. This was previously described in the Parameter Estimation Paper. Our results for GW150914 and LVT151012 have been updated as we have reran with the newer calibration of the data. The new calibration has less uncertainty, which improves the precision of our results, although this is really only significant for the sky localization. Technical details of the analysis are given in Appendix B and results are discussed in Section IV. You may recognise the writing style of these sections.
The probability distributions for the masses are shown below. There is quite a spectrum, from the low mass GW151226, which is consistent with measurements of black holes in X-ray binaries, up to GW150914, which contains the biggest stellar-mass black holes ever observed.
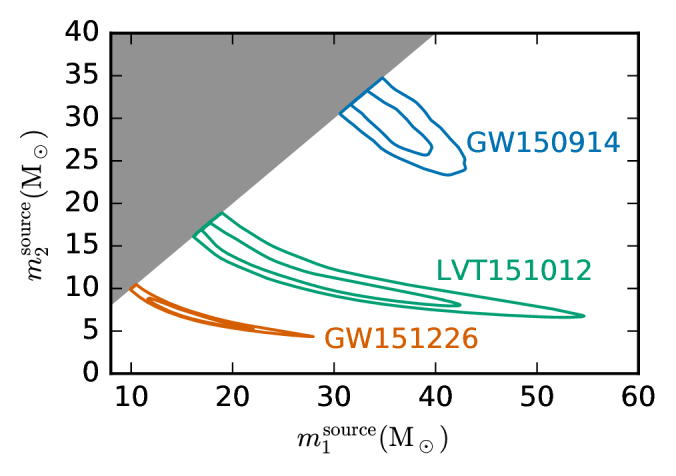
Estimated masses for the two binary black holes for each of the events in O1. The contours mark the 50% and 90% credible regions. The grey area is excluded from our convention that . Part of Figure 4 of the O1 Binary Black Hole Paper.
The distributions for the lower mass GW151226 and LVT151012 follow the curves of constant chirp mass. The uncertainty is greater for LVT151012 as it is a quieter (lower SNR) signal. GW150914 looks a little different, as the merger and ringdown portions of the waveform are more important. These place tighter constraints on the total mass, explaining the shape of the distribution.
Another difference between the lower mass inspiral-dominated signals and the higher mass GW150915 can be seen in the plot below. The shows the probability distributions for the mass ratio and the effective spin parameter
, which is a mass-weighted combination of the spins aligned with the orbital angular momentum. Both play similar parts in determining the evolution of the inspiral, so there are stretching degeneracies for GW151226 and LVT151012, but this isn’t the case for GW150914.
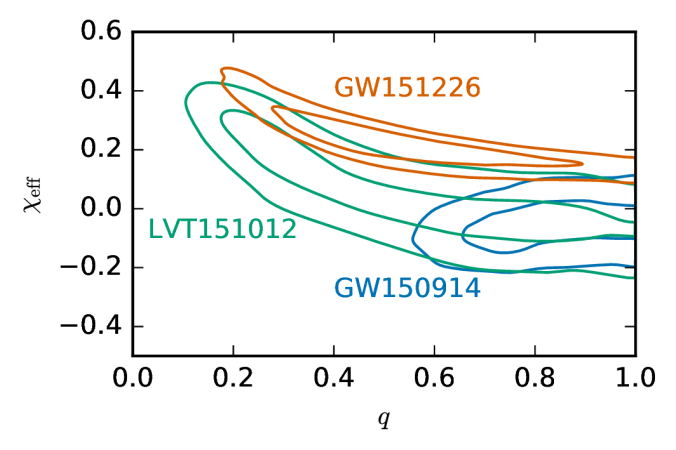
Estimated mass ratios and effective spins
for each of the events in O1. The contours mark the 50% and 90% credible regions. Part of Figure 4 of the O1 Binary Black Hole Paper.
If you look carefully at the distribution of for GW151226, you can see that it doesn’t extend down to zero. You cannot have a non-zero
unless at least one of the black holes is spinning, so this clearly shows the evidence for spin.
The final masses of the remnant black holes are shown below. Each is around 5% less than the total mass of the binary which merged to form it, with the rest radiated away as gravitational waves.
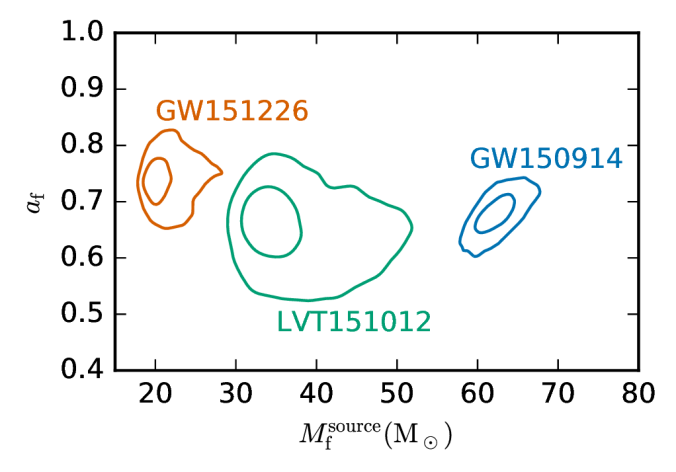
Estimated masses and spins
of the remnant black holes for each of the events in O1. The contours mark the 50% and 90% credible regions. Part of Figure 4 of the O1 Binary Black Hole Paper.
The plot also shows the final spins. These are much better constrained than the component spins as they are largely determined by the angular momentum of the binary as it merged. This is why the spins are all quite similar. To calculate the final spin, we use an updated formula compared to the one in the Parameter Estimation Paper. This now includes the effect of the components’ spin which isn’t aligned with the angular momentum. This doesn’t make much difference for GW150914 or LVT151012, but the change is slightly more for GW151226, as it seems to have more significant component spins.
The luminosity distance for the sources is shown below. We have large uncertainties because the luminosity distance is degenerate with the inclination. For GW151226 and LVT151012 this does result in some beautiful butterfly-like distance–inclination plots. For GW150914, the butterfly only has the face-off inclination wing (probably as consequence of the signal being louder and the location of the source on the sky). The luminosity distances for GW150914 and GW151226 are similar. This may seem odd, because GW151226 is a quieter signal, but that is because it is also lower mass (and so intrinsically quieter).
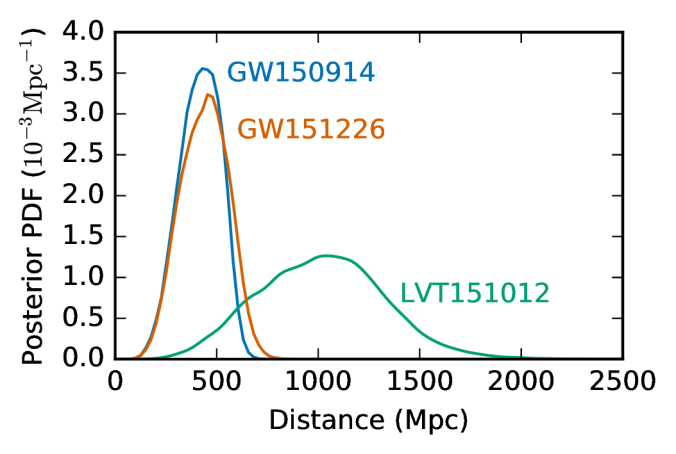
Probability distributions for the luminosity distance of the source of each of the three events in O1. Part of Figure 4 of the O1 Binary Black Hole Paper.
Sky localization is largely determined by the time delay between the two observatories. This is one of the reasons that having a third detector, like Virgo, is an awesome idea. The plot below shows the localization relative to the Earth. You can see that each event has a localization that is part of a ring which is set by the time delay. GW150914 and GW151226 were seen by Livingston first (apparently there is some gloating about this), and LVT151012 was seen by Hanford first.

Estimated sky localization relative to the Earth for each of the events in O1. The contours mark the 50% and 90% credible regions. H+ and L+ mark the locations of the two observatories. Part of Figure 5 of the O1 Binary Black Hole Paper.
Both GW151226 and LVT151012 are nearly overhead. This isn’t too surprising, as this is where the detectors are most sensitive, and so where we expect to make the most detections.
The improvement in the calibration of the data is most evident in the sky localization. For GW150914, the reduction in calibration uncertainty improves the localization by a factor of ~2–3! For LVT151012 it doesn’t make much difference because of its location and because it is a much quieter signal.
The map below shows the localization on the sky (actually where in Universe the signal came from). The maps have rearranged themselves because of the Earth’s rotation (each event was observed at a different sidereal time).
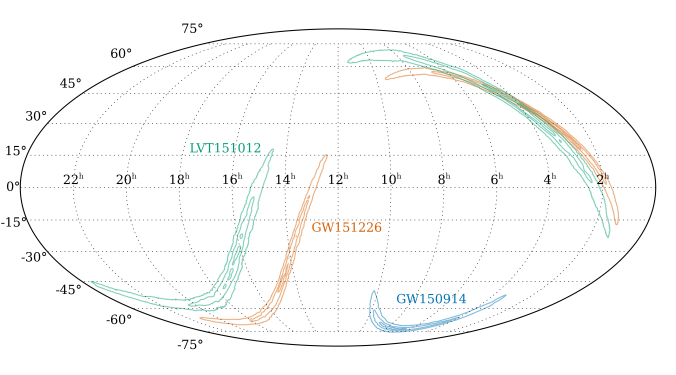
Estimated sky localization (in right ascension and declination) for each of the events in O1. The contours mark the 50% and 90% credible regions. Part of Figure 5 of the O1 Binary Black Hole Paper.
We’re nowhere near localising sources to single galaxies, so we may never know exactly where these signals originated from.
Tests of general relativity
The Testing General Relativity Paper reported several results which compared GW150914 with the predictions of general relativity. Either happily or sadly, depending upon your point of view, it passed them all. In Section V of the paper, we now add GW151226 into the mix. (We don’t add LVT151012 as it’s too quiet to be much use).
A couple of the tests for GW150914 looked at the post-inspiral part of the waveform, looking at the consistency of mass and spin estimates, and trying to match the ringdown frequency. Since GW151226 is lower mass, we can’t extract any meaningful information from the post-inspiral portion of the waveform, and so it’s not worth repeating these tests.
However, the fact that GW151226 has such a lovely inspiral means that we can place some constraints on post-Newtonian parameters. We have lots and lots of cycles, so we are sensitive to any small deviations that arise during inspiral.
The plot below shows constraints on deviations for a set of different waveform parameters. A deviation of zero indicates the value in general relativity. The first four boxes (for parameters referred to as in the Testing General Relativity Paper) are parameters that affect the inspiral. The final box on the right is for parameters which impact the merger and ringdown. The top row shows results for GW150914, these are updated results using the improved calibrated data. The second row shows results for GW151226, and the bottom row shows what happens when you combine the two.
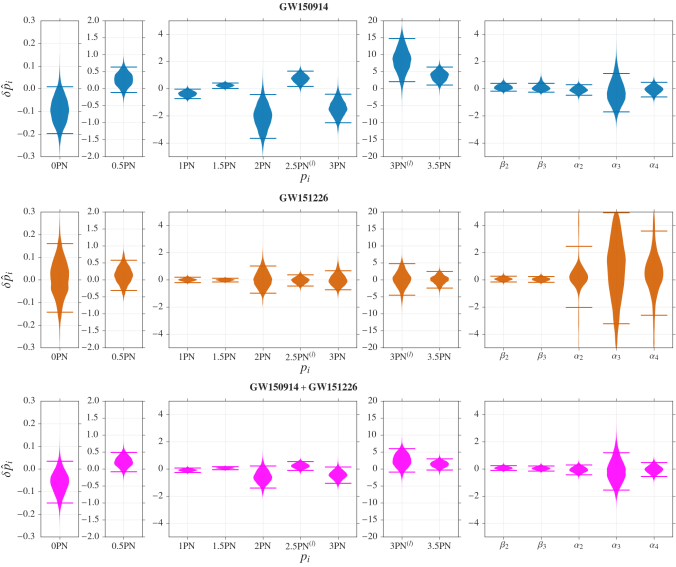
Probability distributions for waveform parameters. The top row shows bounds from just GW150914, the second from just GW151226, and the third from combining the two. A deviation of zero is consistent with general relativity. Figure 6 from the O1 Binary Black hole Paper.
All the results are happily about zero. There were a few outliers for GW150914, but these are pulled back in by GW151226. We see that GW151226 dominates the constraints on the inspiral parameters, but GW150914 is more important for the merger–ringdown parameters.
Again, Einstein’s theory passes the test. There is no sign of inconsistency (yet). It’s clear that adding more results greatly improves our sensitivity to these parameters, so these tests will continue put general relativity through tougher and tougher tests.
Rates
We have a small number of events, around 2.9 in total, so any estimates of how often binary black holes merge will be uncertain. Of course, just because something is tricky, it doesn’t mean we won’t give it a go! The Rates Paper discussed estimates after the first 16 days of coincident data, when we had just 1.9 events. Appendix C gives technical details and Section VI discusses results.
The whole of O1 is about 52 days’ worth of coincident data. It’s therefore about 3 times as long as the initial stretch. in that time we’ve observed about 3/2 times as many events. Therefore, you might expect that the event rate is about 1/2 of our original estimates. If you did, get yourself a cookie, as you are indeed about right!
To calculate the rates we need to assume something about the population of binary black holes. We use three fiducial distributions:
- We assume that binary black holes are either like GW150914, LVT151012 or GW151226. This event-based rate is different from the previous one as it now includes an extra class for GW151226.
- A flat-in-the-logarithm-of-masses distribution, which we expect gives a sensible lower bound on the rate.
- A power law slope for the larger black hole of
, which we expect gives a sensible upper bound on the rate.
We find that the rates are 1. , 2.
, and 3.
. As expected, the first rate is nestled between the other two.
Despite the rates being lower, there’s still a good chance we could see 10 events by the end of O2 (although that will depend on the sensitivity of the detectors).
A new results that is included in with the rates, is a simple fit for the distribution of black hole masses [bonus note]. The method is described in Appendix D. It’s just a repeated application of Bayes’ theorem to go from the masses we measured from the detected sources, to the distribution of masses of the entire population.
We assume that the mass of the larger black hole is distributed according to a power law with index , and that the less massive black hole has a mass uniformly distributed in mass ratio, down to a minimum black hole mass of
. The cut-off, is the edge of a speculated mass gap between neutron stars and black holes.
We find that . This has significant uncertainty, so we can’t say too much yet. This is a slightly steeper slope than used for the power-law rate (although entirely consistent with it), which would nudge the rates a little lower. The slope does fit in with fits to the distribution of masses in X-ray binaries. I’m excited to see how O2 will change our understanding of the distribution.
Astrophysical implications
With the announcement of GW150914, the Astrophysics Paper reviewed predictions for binary black holes in light of the discovery. The high masses of GW150914 indicated a low metallicity environment, perhaps no more than half of solar metallicity. However, we couldn’t tell if GW150914 came from isolated binary evolution (two stars which have lived and died together) or a dynamical interaction (probably in a globular cluster).
Since then, various studies have been performed looking at both binary evolution (Eldridge & Stanway 2016; Belczynski et al. 2016; de Mink & Mandel 2016; Hartwig et al. 2016; Inayoshi et al. 2016; Lipunov et al. 2016) and dynamical interactions (O’Leary, Meiron & Kocsis 2016; Mapelli 2016; Rodriguez et al. 2016), even considering binaries around supermassive black holes (Bartos et al. 2016; Stone, Metzger & Haiman 2016). We don’t have enough information to tell the two pathways apart. GW151226 gives some new information. Everything is reviewed briefly in Section VII.
GW151226 and LVT151012 are lower mass systems, and so don’t need to come from as low a metallicity environment as GW150914 (although they still could). Both are also consistent with either binary evolution or dynamical interactions. However, the low masses of GW151226 mean that it probably does not come from one particular binary formation scenario, chemically homogeneous evolution, and it is less likely to come from dynamical interactions.
Building up a population of sources, and getting better measurements of spins and mass ratios will help tease formation mechanisms apart. That will take a while, but perhaps it will be helped if we can do multi-band gravitational-wave astronomy with eLISA.
This section also updates predictions from the Stochastic Paper for the gravitational-wave background from binary black holes. There’s a small change from an energy density of at a frequency of 25 Hz to
. This might be measurable after a few years at design sensitivity.
Conclusion
We are living in the future. We may not have hoverboards, but the era of gravitational-wave astronomy is here. Not in 20 years, not in the next decade, not in five more years, now. LIGO has not just opened a new window, it’s smashed the window and jumped through it just before the explosion blasts the side off the building. It’s so exciting that I can’t even get my metaphors straight. The introductory paragraphs of papers on gravitational-wave astronomy will never be the same again.
Although we were lucky to discover GW150914, it wasn’t just a fluke. Binary black coalescences aren’t that rare and we should be detecting more. Lots more. You know that scene in a movie where the heroes have defeated a wave of enemies and then the camera pans back to show the approaching hoard that stretches to the horizon? That’s where we are now. O2 is coming. The second observing run, will start later this year, and we expect we’ll be adding many entries to our list of binary black holes.
We’re just getting started with LIGO and Virgo. There’ll be lots more science to come.
If you made it this far, you deserve a biscuit. A fancy one too, not just a digestive.
Or, if you’re hungry for more, here are some blogs from my LIGO colleagues
- Daniel Williams (a PhD student at University of Glasgow)
- Matt Pitkin (who is hunting for continuous gravitational waves)
- Shane Larson (who is also investigating mutli-band gravitational-wave astronomy)
- Amber Sturver (who works at the Livingston Observatory)
My group at Birmingham also made some short reaction videos (I’m too embarrassed to watch mine).
Bonus notes
Christmas cease-fire
In the run-up to the holidays, there were lots of emails that contained phrases like “will have to wait until people get back from holidays” or “can’t reply as the group are travelling and have family commitments”. No-one ever said that they were taking a holiday, but just that it was happening in general, so we’d all have to wait for a couple of weeks. No-one ever argued with this, because, of course, while you were waiting for other people to do things, there was nothing you could do, and so you might as well take some time off. And you had been working really hard, so perhaps an evening off and an extra slice of cake was deserved…
Rather guiltily, I must confess to ignoring the first few emails on Boxing Day. (Although I saw them, I didn’t read them for reasons of plausible deniability). I thought it was important that my laptop could have Boxing Day off. Thankfully, others in the Collaboration were more energetic and got things going straight-away.
Naming
Gravitational-wave candidates (or at least the short ones from merging binary black holes which we have detected so far), start off life named by a number in our database. This event started life out as G211117. After checks and further analysis, to make sure we can’t identify any environmental effects which could have caused the detector to misbehave, candidates are renamed. Those which are significant enough to be claimed as a detection get the Gravitational Wave (GW) prefix. Those we are less certain of get the LIGO–Virgo Trigger (LVT) prefix. The rest of the name is the date in Coordinated Universal Time (UTC). The new detection is GW151226.
Informally though, it is the Boxing Day Event. I’m rather impressed that this stuck as the Collaboration is largely US based: it was still Christmas Day in the US when the detection was made, and Americans don’t celebrate Boxing Day anyway.
Other searches
We are now publishing the results of the O1 search for binary black holes with a template bank which goes up to total observed binary masses of . Therefore we still have to do the same about searches for anything else. The results from searches for other compact binaries should appear soon (binary neutron star and neutron star–black hole upper limits; intermediate mass black hole binary upper limits). It may be a while before we have all the results looking for continuous waves.
Matched filtering
The compact binary coalescence search uses matched filtering to hunt for gravitational waves. This is a well established technique in signal processing. You have a template signal, and you see how this correlates with the data. We use the detectors’ sensitivity to filter the data, so that we give more weight to bits which match where we are sensitive, and little weight to matches where we have little sensitivity.
I imagine matched filtering as similar to how I identify a piece of music: I hear a pattern of notes and try to compare to things I know. Dum-dum-dum-daah? Beethoven’s Fifth.
Filtering against a large number of templates takes a lot of computational power, so we need to be cunning as to which templates we include. We don’t want to miss anything, so we need enough templates to cover all possibilities, but signals from similar systems can look almost identical, so we just need one representative template included in the bank. Think of trying to pick out Under Pressure, you could easily do this with a template for Ice Ice Baby, and you don’t need both Mr Brightside and Ode to Joy.
It doesn’t matter if the search doesn’t pick out a template that perfectly fits the properties of the source, as this is what parameter estimation is for.
The figure below shows how effective matched filtering can be.
- The top row shows the data from the two interferometers. It’s been cleaned up a little bit for the plot (to keep the experimentalists happy), but you can see that the noise in the detectors is seemingly much bigger than the best match template (shown in black, the same for both detectors).
- The second row shows the accumulation of signal-to-noise ratio (SNR). If you correlate the data with the template, you see that it matches the template, and keeps matching the template. This is the important part, although, at any moment it looks like there’s just random wibbles in the detector, when you compare with a template you find that there is actually a signal which evolves in a particular way. The SNR increases until the signal stops (because the black holes have merged). It is a little lower in the Livinston detector as this was slightly less sensitive around the time of the Boxing Day Event.
- The third row shows how much total SNR you would get if you moved the best match template around in time. There’s a clear peak. This is trying to show that the way the signal changes is important, and you wouldn’t get a high SNR when the signal isn’t there (you would normally expect it to be about 1).
- The final row shows the amount of energy at a particular frequency at a particular time. Compact binary coalescences have a characteristic chirp, so you would expect a sweep from lower frequencies up to higher frequencies. You can just about make it out in these plots, but it’s not obvious as for GW150914. This again shows the value of matched filtering, but it also shows that there’s no other weird glitchy stuff going on in the detectors at the time.
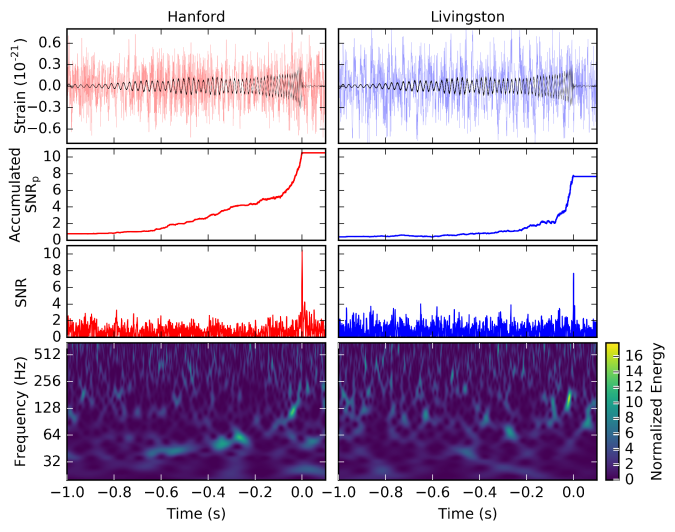
Observation of The Boxing Day Event in LIGO Hanford and LIGO Livingston. The top row shows filtered data and best match template. The second row shows how this template accumulates signal-to-noise ratio. The third row shows signal-to-noise ratio of this template at different end times. The fourth row shows a spectrogram of the data. Figure 1 of the Boxing Day Discovery Paper.
Electromagnetic and neutrino follow-up
Reports by electromagnetic astronomers on their searches for counterparts so far are:
- CALET—an X-ray and gamma-ray search. This team also have a paper on their analysis and upper limits for GW151226, GW170104, GW170608, GW170814 and GW170817.
- Dark Energy Camera—an optical search.
- Fermi GBM & LAT—an X-ray and gamma-ray search for counterparts to GW151226 and LVT151012.
- Jansky Very Large Array—a radio search for counterparts to GW150914 and GW151226. A separate effort later followed up the most probable 100 square degrees later, as a test of a new on-the-fly mosaicing technique.
- J-GEM—an optical and near-infrared survey.
- Liverpool Telescope—an optical and near-infrared search for counterparts to GW150914 and GW151226.
- MAXI—an X-ray monitor on the International Space Station.
- Pan-STARRS & PESSTO—an optical search which didn’t find a counterpart, but did find an unusual Type Ibn supernova.
- Swift—an X-ray search.
- GRAWITA—an optical search.
Reports by neutrino astronomers are:
- ANTARES and IceCube—a search for high-energy neutrinos (above 100 GeV) coincident with LVT151012 or GW151226.
- KamLAND—a search for neutrinos (1.8 MeV to 111 MeV) coincident with GW150914, LVT151012 or GW151226.
- Pierre Auger Observatory—a search for ultra high-energy (above 100 PeV) neutrinos coincident with GW150914, LVT151012 or GW151226.
- Super-Kamiokande—a search for neutrinos (of a wide range of energies, from 3.5 MeV to 100 PeV) coincident with GW150914 or GW151226.
- Borexino—a search for low-energy (250 keV to 15 MeV) neutrinos coincident with GW150914, GW151226 and GW170104.
- NOvA—a search for neutrinos and cosmic rays (or a wide range of energies, from 10 MeV to over a GeV) coincident with all events from O1 and O2, plus triggers from O3.
No counterparts have been claimed, which isn’t surprising for a binary black hole coalescence.
Rounding
In various places, the mass of the smaller black hole is given as . The median should really round to
as to three significant figures it is
. This really confused everyone though, as with rounding you’d have a binary with components of masses
and
and total mass
. Rounding is a pain! Fortunately,
lies well within the uncertainty: the 90% range is
.
Black holes are massive
I tried to find a way to convert the mass of the final black hole into every day scales. Unfortunately, the thing is so unbelievably massive, it just doesn’t work: it’s no use relating it to elephants or bowling balls. However, I did have some fun looking up numbers. Currently, it costs about £2 to buy a 180 gram bar of Cadbury’s Bourneville. Therefore, to buy an equivalent amount of dark chocolate would require everyone on Earth to save up for about 600 millions times the age of the Universe (assuming GDP stays constant). By this point, I’m sure the chocolate will be past its best, so it’s almost certainly a big waste of time.
Maximum minimum spin
One of the statistics people really seemed to latch on to for the Boxing Day Event was that at least one of the binary black holes had to have a spin of greater than 0.2 with 99% probability. It’s a nice number for showing that we have a preference for some spin, but it can be a bit tricky to interpret. If we knew absolutely nothing about the spins, then we would have a uniform distribution on both spins. There’d be a 10% chance that the spin of the more massive black hole is less than 0.1, and a 10% chance that the spin of the other black hole is less than 0.1. Hence, there’s a 99% probability that there is at least one black hole with spin greater than 0.1, even though we have no evidence that the black holes are spinning (or not). Really, you need to look at the full probability distributions for the spins, and not just the summary statistics, to get an idea of what’s going on.
Just one more thing…
The fit for the black hole mass distribution was the last thing to go in the paper. It was a bit frantic to get everything reviewed in time. In the last week, there were a couple of loud exclamations from the office next to mine, occupied by John Veitch, who as one of the CBC chairs has to keep everything and everyone organised. (I’m not quite sure how John still has so much of his hair). It seems that we just can’t stop doing science. There is a more sophisticated calculation in the works, but the foot was put down that we’re not trying to cram any more into the current papers.
Fantastic news Christopher! Congratulations on yet another great discovery from the Carolian Astronomy Society in Kidderminster. I’ve just heard about the Cambridge paper by Gerosa and Moore on Black Hole Kicks and the new opportunities that it offers for gravitational wave astronomy. Pity that they regard LIGO as not sensitive enough. Still, eLISA is making good progress.
Best wishes
David Hodgson
LikeLike
It is good news about LISA Pathfinder, so things do look good for eLISA. There are many things more exciting than kicks it can measure though. A popular topic at the moment is looking at the eccentricity of the orbits of stellar-mass black hole binaries (Nishizawa et al. 2016; Breivik et al. 2016). This is too small for LIGO to measure, but could be measured with eLISA. Doing so could help us pin down how binary black holes form.
LikeLike