Dirichlet Process Gaussian-mixture model: An application to localizing coalescing binary neutron stars with gravitational-wave observations

August 10, 2018August 20, 2019 / CPLB / Leave a comment

Where do gravitational waves like GW170817 come from? Using our network of detectors, we cannot pinpoint a source, but we can make a good estimate—the amplitude of the signal tells us about the distance; the time delay between the signal arriving at different detectors, and relative amplitudes of the signal in different detectors tells us about the sky position (see the excellent video by Leo Singer below).

In this paper we look at full three-dimensional localization of gravitational-wave sources; we important a (rather cunning) technique from computer vision to construct a probability distribution for the source’s location, and then explore how well we could localise a set of simulated binary neutron stars. Knowing the source location enables lots of cool science. First, it aids direct follow-up observations with non-gravitational-wave observatories, searching for electromagnetic or neutrino counterparts. It’s especially helpful if you can cross-reference with galaxy catalogues, to find the most probable source locations (this technique was used to find the kilonova associated with GW170817). Even without finding a counterpart, knowing the most probable host galaxy helps us figure out how the source formed (have lots of stars been born recently, or are all the stars old?), and allows us measure the expansion of the Universe. Having a reliable technique to reconstruct source locations is useful!

This was a fun paper to write [bonus note]. I’m sure it will be valuable, both for showing how to perform this type of reconstruction of a multi-dimensional probability density, and for its implications for source localization and follow-up of gravitational-wave signals. I go into details of both below, first discussing our statistical model (this is a bit technical), then looking at our results for a set of binary neutron stars (which have implications for hunting for counterparts) .

Dirichlet process Gaussian mixture model

When we analyse gravitational-wave data to infer the source properties (location, masses, etc.), we map out parameter space with a set of samples: a list of points in the parameter space, with there being more around more probable locations and fewer in less probable locations. These samples encode everything about the probability distribution for the different parameters, we just need to extract it…

For our application, we want a nice smooth probability density. How do we convert a bunch of discrete samples to a smooth distribution? The simplest thing is to bin the samples. However, picking the right bin size is difficult, and becomes much harder in higher dimensions. Another popular option is to use kernel density estimation. This is better at ensuring smooth results, but you now have to worry about the size of your kernels.

Our approach is in essence to use a kernel density estimate, but to learn the size and position of the kernels (as well as the number) from the data as an extra layer of inference. The “Gaussian mixture model” part of the name refers to the kernels—we use several different Gaussians. The “Dirichlet process” part refers to how we assign their properties (their means and standard deviations). What I really like about this technique, as opposed to the usual rule-of-thumb approaches used for kernel density estimation, is that it is well justified from a theoretical point of view.

I hadn’t come across a Dirchlet process before. Section 2 of the paper is a walkthrough of how I built up an understanding of this mathematical object, and it contains lots of helpful references if you’d like to dig deeper.

In our application, you can think of the Dirichlet process as being a probability distribution for probability distributions. We want a probability distribution describing the source location. Given our samples, we infer what this looks like. We could put all the probability into one big Gaussian, or we could put it into lots of little Gaussians. The Gaussians could be wide or narrow or a mix. The Dirichlet distribution allows us to assign probabilities to each configuration of Gaussians; for example, if our samples are all in the northern hemisphere, we probably want Gaussians centred around there, rather than in the southern hemisphere.

With the resulting probability distribution for the source location, we can quickly evaluate it at a single point. This means we can rapidly produce a list of most probable source galaxies—extremely handy if you need to know where to point a telescope before a kilonova fades away (or someone else finds it).

Gravitational-wave localization

To verify our technique works, and develop an intuition for three-dimensional localizations, we used studied a set of simulated binary neutron star signals created for the First 2 Years trilogy of papers. This data set is well studied now, it illustrates performance it what we anticipated to be the first two observing runs of the advanced detectors, which turned out to be not too far from the truth. We have previously looked at three-dimensional localizations for these signals using a super rapid approximation.

The plots below show how well we could localise the sources of our binary neutron star sources. Specifically, the plots show the size of the volume which has a 90% probability of containing the source verses the signal-to-noise ratio (the loudness) of the signal. Typically, volumes are $10^4$ – $10^5~\mathrm{Mpc}^3$ , which is about $10^{68}$ – $10^{69}$ Olympic swimming pools. Such a volume would contain something like $100$ – $1000$ galaxies.

Localization volume as a function of signal-to-noise ratio. The top panel shows results for two-detector observations: the LIGO-Hanford and LIGO-Livingston (HL) network similar to in the first observing run, and the LIGO and Virgo (HLV) network similar to the second observing run. The bottom panel shows all observations for the HLV network including those with all three detectors which are colour coded by the fraction of the total signal-to-noise ratio from Virgo. In both panels, there are fiducial lines scaling inversely with the sixth power of the signal-to-noise ratio. Adapted from Fig. 4 of Del Pozzo et al. (2018).

Looking at the results in detail, we can learn a number of things

The localization volume is roughly inversely proportional to the sixth power of the signal-to-noise ratio [bonus note]. Loud signals are localized much better than quieter ones!
The localization dramatically improves when we have three-detector observations. The extra detector improves the sky localization, which reduces the localization volume.
To get the benefit of the extra detector, the source needs to be close enough that all the detectors could get a decent amount of the signal-to-noise ratio. In our case, Virgo is the least sensitive, and we see the the best localizations are when it has a fair share of the signal-to-noise ratio.
Considering the cases where we only have two detectors, localization volumes get bigger at a given signal-to-noise ration as the detectors get more sensitive. This is because we can detect sources at greater distances.

Putting all these bits together, I think in the future, when we have lots of detections, it would make most sense to prioritise following up the loudest signals. These are the best localised, and will also be the brightest since they are the closest, meaning there’s the greatest potential for actually finding a counterpart. As the sensitivity of the detectors improves, its only going to get more difficult to find a counterpart to a typical gravitational-wave signal, as sources will be further away and less well localized. However, having more sensitive detectors also means that we are more likely to have a really loud signal, which should be really well localized.

Left: Localization (yellow) with a network of two low-sensitivity detectors. The sky location is uncertain, but we know the source must be nearby. Right: Localization (green) with a network of three high-sensitivity detectors. We have good constraints on the source location, but it could now be at a much greater range of distances. Not to scale.

Using our localization volumes as a guide, you would only need to search one galaxy to find the true source in about 7% of cases with a three-detector network similar to at the end of our second observing run. Similarly, only ten would need to be searched in 23% of cases. It might be possible to get even better performance by considering which galaxies are most probable because they are the biggest or the most likely to produce merging binary neutron stars. This is definitely a good approach to follow.

Three-dimensional localization with galaxy catalgoue

Galaxies within the 90% credible volume of an example simulated source, colour coded by probability. The galaxies are from the GLADE Catalog; incompleteness in the plane of the Milky Way causes the missing wedge of galaxies. The true source location is marked by a cross [bonus note]. Part of Figure 5 of Del Pozzo et al. (2018).

arXiv: 1801.08009 [astro-ph.IM]
Journal: Monthly Notices of the Royal Astronomical Society; 479(1):601–614; 2018
Code: 3d_volume
Buzzword bingo: Interdisciplinary (we worked with computer scientist Tom Haines); machine learning (the inference involving our Dirichlet process Gaussian mixture model); multimessenger astronomy (as our results are useful for following up gravitational-wave signals in the search for counterparts)

Bonus notes

Writing

We started writing this paper back before the first observing run of Advanced LIGO. We had a pretty complete draft on Friday 11 September 2015. We just needed to gather together a few extra numbers and polish up the figures and we’d be done! At 10:50 am on Monday 14 September 2015, we made our first detection of gravitational waves. The paper was put on hold. The pace of discoveries over the coming years meant we never quite found enough time to get it together—I’ve rewritten the introduction a dozen times. It’s extremely satisfying to have it done. This is a shame, as it meant that this study came out much later than our other three-dimensional localization study. The delay has the advantage of justifying one of my favourite acknowledgement sections.

Sixth power

We find that the localization volume $\Delta V$ is inversely proportional to the sixth power of the signal-to-noise ration $\varrho$ . This is what you would expect. The localization volume depends upon the angular uncertainty on the sky $\Delta \Omega$ , the distance to the source $D$ , and the distance uncertainty $\Delta D$ ,

$\Delta V \sim D^2 \Delta \Omega \Delta D$ .

Typically, the uncertainty on a parameter (like the masses) scales inversely with the signal-to-noise ratio. This is the case for the logarithm of the distance, which means

$\displaystyle \frac{\Delta D}{D} \propto \varrho^{-1}$ .

The uncertainty in the sky location (being two dimensional) scales inversely with the square of the signal-to-noise ration,

$\Delta \Omega \propto \varrho^{-2}$ .

The signal-to-noise ratio itself is inversely proportional to the distance to the source (sources further way are quieter. Therefore, putting everything together gives

$\Delta V \propto \varrho^{-6}$ .

Treasure

We all know that treasure is marked by a cross. In the case of a binary neutron star merger, dense material ejected from the neutron stars will decay to heavy elements like gold and platinum, so there is definitely a lot of treasure at the source location.

GW150914—The papers II

December 10, 2016February 9, 2020 / CPLB / Leave a comment

GW150914, The Event to its friends, was our first direct observation of gravitational waves. To accompany the detection announcement, the LIGO Scientific & Virgo Collaboration put together a suite of companion papers, each looking at a different aspect of the detection and its implications. Some of the work we wanted to do was not finished at the time of the announcement; in this post I’ll go through the papers we have produced since the announcement.

The papers

I’ve listed the papers below in an order that makes sense to me when considering them together. Each started off as an investigation to check that we really understood the signal and were confident that the inferences made about the source were correct. We had preliminary results for each at the time of the announcement. Since then, the papers have evolved to fill different niches [bonus points note].

13. The Basic Physics Paper

Title: The basic physics of the binary black hole merger GW150914
arXiv: 1608.01940 [gr-qc]
Journal: Annalen der Physik; 529(1–2):1600209(17); 2017

The Event was loud enough to spot by eye after some simple filtering (provided that you knew where to look). You can therefore figure out some things about the source with back-of-the-envelope calculations. In particular, you can convince yourself that the source must be two black holes. This paper explains these calculations at a level suitable for a keen high-school or undergraduate physics student.

More details: The Basic Physics Paper summary

14. The Precession Paper

Title: Improved analysis of GW150914 using a fully spin-precessing waveform model
arXiv: 1606.01210 [gr-qc]
Journal: Physical Review X; 6(4):041014(19); 2016

To properly measure the properties of GW150914’s source, you need to compare the data to predicted gravitational-wave signals. In the Parameter Estimation Paper, we did this using two different waveform models. These models include lots of features binary black hole mergers, but not quite everything. In particular, they don’t include all the effects of precession (the wibbling of the orbit because of the black holes spins). In this paper, we analyse the signal using a model that includes all the precession effects. We find results which are consistent with our initial ones.

More details: The Precession Paper summary

15. The Systematics Paper

Title: Effects of waveform model systematics on the interpretation of GW150914
arXiv: 1611.07531 [gr-qc]
Journal: Classical & Quantum Gravity; 34(10):104002(48); 2017
LIGO science summary: Checking the accuracy of models of gravitational waves for the first measurement of a black hole merger

To check how well our waveform models can measure the properties of the source, we repeat the parameter-estimation analysis on some synthetic signals. These fake signals are calculated using numerical relativity, and so should include all the relevant pieces of physics (even those missing from our models). This paper checks to see if there are any systematic errors in results for a signal like GW150914. It looks like we’re OK, but this won’t always be the case.

More details: The Systematics Paper summary

16. The Numerical Relativity Comparison Paper

Title: Directly comparing GW150914 with numerical solutions of Einstein’s equations for binary black hole coalescence
arXiv: 1606.01262 [gr-qc]
Journal: Physical Review D; 94(6):064035(30); 2016
LIGO science summary: Directly comparing the first observed gravitational waves to supercomputer solutions of Einstein’s theory

Since GW150914 was so short, we can actually compare the data directly to waveforms calculated using numerical relativity. We only have a handful of numerical relativity simulations, but these are enough to give an estimate of the properties of the source. This paper reports the results of this investigation. Unsurprisingly, given all the other checks we’ve done, we find that the results are consistent with our earlier analysis.

If you’re interested in numerical relativity, this paper also gives a nice brief introduction to the field.

More details: The Numerical Relativity Comparison Paper summary

The Basic Physics Paper

Synopsis: Basic Physics Paper
Read this if: You are teaching a class on gravitational waves
Favourite part: This is published in Annalen der Physik, the same journal that Einstein published some of his monumental work on both special and general relativity

It’s fun to play with LIGO data. The Gravitational Wave Open Science Center (GWOSC), has put together a selection of tutorials to show you some of the basics of analysing signals; we also have papers which introduce gravitational wave data analysis. I wouldn’t blame you if you went of to try them now, instead of reading the rest of this post. Even though it would mean that no-one read this sentence. Purple monkey dishwasher.

The GWOSC tutorials show you how to make your own version of some of the famous plots from the detection announcement. This paper explains how to go from these, using the minimum of theory, to some inferences about the signal’s source: most significantly that it must be the merger of two black holes.

GW150914 is a chirp. It sweeps up from low frequency to high. This is what you would expect of a binary system emitting gravitational waves. The gravitational waves carry away energy and angular momentum, causing the binary’s orbit to shrink. This means that the orbital period gets shorter, and the orbital frequency higher. The gravitational wave frequency is twice the orbital frequency (for circular orbits), so this goes up too.

The rate of change of the frequency depends upon the system’s mass. To first approximation, it is determined by the chirp mass,

$\displaystyle \mathcal{M} = \frac{(m_1 m_2)^{3/5}}{(m_1 + m_2)^{1/5}}$ ,

where $m_1$ and $m_2$ are the masses of the two components of the binary. By looking at the signal (go on, try the GWOSC tutorials), we can estimate the gravitational wave frequency $f_\mathrm{GW}$ at different times, and so track how it changes. You can rewrite the equation for the rate of change of the gravitational wave frequency $\dot{f}_\mathrm{GW}$ , to give an expression for the chirp mass

$\displaystyle \mathcal{M} = \frac{c^3}{G}\left(\frac{5}{96} \pi^{-8/3} f_\mathrm{GW}^{-11/3} \dot{f}_\mathrm{GW}\right)^{3/5}$ .

Here $c$ and $G$ are the speed of light and the gravitational constant, which usually pop up in general relativity equations. If you use this formula (perhaps fitting for the trend $f_\mathrm{GW}$ ) you can get an estimate for the chirp mass. By fiddling with your fit, you’ll see there is some uncertainty, but you should end up with a value around $30 M_\odot$ [bonus note].

Next, let’s look at the peak gravitational wave frequency (where the signal is loudest). This should be when the binary finally merges. The peak is at about $150~\mathrm{Hz}$ . The orbital frequency is half this, so $f_\mathrm{orb} \approx 75~\mathrm{Hz}$ . The orbital separation $R$ is related to the frequency by

$\displaystyle R = \left[\frac{GM}{(2\pi f_\mathrm{orb})^2}\right]^{1/3}$ ,

where $M = m_1 + m_2$ is the binary’s total mass. This formula is only strictly true in Newtonian gravity, and not in full general relativity, but it’s still a reasonable approximation. We can estimate a value for the total mass from our chirp mass; if we assume the two components are about the same mass, then $M = 2^{6/5} \mathcal{M} \approx 70 M_\odot$ . We now want to compare the binary’s separation to the size of black hole with the same mass. A typical size for a black hole is given by the Schwarzschild radius

$\displaystyle R_\mathrm{S} = \frac{2GM}{c^2}$ .

If we divide the binary separation by the Schwarzschild radius we get the compactness $\mathcal{R} = R/R_\mathrm{S} \approx 1.7$ . A compactness of $\sim 1$ could only happen for black holes. We could maybe get a binary made of two neutron stars to have a compactness of $\sim2$ , but the system is too heavy to contain two neutron stars (which have a maximum mass of about $3 M_\odot$ ). The system is so compact, it must contain black holes!

What I especially like about the compactness is that it is unaffected by cosmological redshifting. The expansion of the Universe will stretch the gravitational wave, such that the frequency gets lower. This impacts our estimates for the true orbital frequency and the masses, but these cancel out in the compactness. There’s no arguing that we have a highly relativistic system.

You might now be wondering what if we don’t assume the binary is equal mass (you’ll find it becomes even more compact), or if we factor in black hole spin, or orbital eccentricity, or that the binary will lose mass as the gravitational waves carry away energy? The paper looks at these and shows that there is some wiggle room, but the signal really constrains you to have black holes. This conclusion is almost as inescapable as a black hole itself.

There are a few things which annoy me about this paper—I think it could have been more polished; “Virgo” is improperly capitalised on the author line, and some of the figures are needlessly shabby. However, I think it is a fantastic idea to put together an introductory paper like this which can be used to show students how you can deduce some properties of GW150914’s source with some simple data analysis. I’m happy to be part of a Collaboration that values communicating our science to all levels of expertise, not just writing papers for specialists!

During my undergraduate degree, there was only a single lecture on gravitational waves [bonus note]. I expect the topic will become more popular now. If you’re putting together such a course and are looking for some simple exercises, this paper might come in handy! Or if you’re a student looking for some project work this might be a good starting reference—bonus points if you put together some better looking graphs for your write-up.

If this paper has whetted your appetite for understanding how different properties of the source system leave an imprint in the gravitational wave signal, I’d recommend looking at the Parameter Estimation Paper for more.

The Precession Paper

Synopsis: Precession Paper
Read this if: You want our most detailed analysis of the spins of GW150914’s black holes
Favourite part: We might have previously over-estimated our systematic error

The Basic Physics Paper explained how you could work out some properties of GW150914’s source with simple calculations. These calculations are rather rough, and lead to estimates with large uncertainties. To do things properly, you need templates for the gravitational wave signal. This is what we did in the Parameter Estimation Paper.

In our original analysis, we used two different waveforms:

The first we referred to as EOBNR, short for the lengthy technical name SEOBNRv2_ROM_DoubleSpin. In short: This includes the spins of the two black holes, but assumes they are aligned such that there’s no precession. In detail: The waveform is calculated by using effective-one-body dynamics (EOB), an approximation for the binary’s motion calculated by transforming the relevant equations into those for a single object. The S at the start stands for spin: the waveform includes the effects of both black holes having spins which are aligned (or antialigned) with the orbital angular momentum. Since the spins are aligned, there’s no precession. The EOB waveforms are tweaked (or calibrated, if you prefer) by comparing them to numerical relativity (NR) waveforms, in particular to get the merger and ringdown portions of the waveform right. While it is easier to solve the EOB equations than full NR simulations, they still take a while. To speed things up, we use a reduced-order model (ROM), a surrogate model constructed to match the waveforms, so we can go straight from system parameters to the waveform, skipping calculating the dynamics of the binary.
The second we refer to as IMRPhenom, short for the technical IMRPhenomPv2. In short: This waveform includes the effects of precession using a simple approximation that captures the most important effects. In detail: The IMR stands for inspiral–merger–ringdown, the three phases of the waveform (which are included in in the EOBNR model too). Phenom is short for phenomenological: the waveform model is constructed by tuning some (arbitrary, but cunningly chosen) functions to match waveforms calculated using a mix of EOB, NR and post-Newtonian theory. This is done for black holes with (anti)aligned spins to first produce the IMRPhenomD model. This is then twisted up, to include the dominant effects of precession to make IMRPhenomPv2. This bit is done by combining the two spins together to create a single parameter, which we call $\chi_\mathrm{p}$ , which determines the amount of precession. Since we are combining the two spins into one number, we lose a bit of the richness of the full dynamics, but we get the main part.

The EOBNR and IMRPhenom models are created by different groups using different methods, so they are useful checks of each other. If there is an error in our waveforms, it would lead to systematic errors in our estimated paramters

In this paper, we use another waveform model, a precessing EOBNR waveform, technically known as SEOBNRv3. This model includes all the effects of precession, not just the simple model of the IMRPhenom model. However, it is also computationally expensive, meaning that the analysis takes a long time (we don’t have a ROM to speed things up, as we do for the other EOBNR waveform)—each waveform takes over 20 times as long to calculate as the IMRPhenom model [bonus note].

Our results show that all three waveforms give similar results. The precessing EOBNR results are generally more like the IMRPhenom results than the non-precessing EOBNR results are. The plot below compares results from the different waveforms [bonus note].

Comparison of results from non-precessing EOBNR, precessing IMRPhenom and precessing EOBNR waveforms

Comparison of parameter estimates for GW150914 using different waveform models. The bars show the 90% credible intervals, the dark bars show the uncertainty on the 5%, 50% and 95% quantiles from the finite number of posterior samples. The top bar is for the non-precessing EOBNR model, the middle is for the precessing IMRPhenom model, and the bottom is for the fully precessing EOBNR model. Figure 1 of the Precession Paper; see Figure 9 for a comparison of averaged EOBNR and IMRPhenom results, which we have used for our overall results.

We had used the difference between the EOBNR and IMRPhenom results to estimate potential systematic error from waveform modelling. Since the two precessing models are generally in better agreement, we have may have been too pessimistic here.

The main difference in results is that our new refined analysis gives tighter constraints on the spins. From the plot above you can see that the uncertainty for the spin magnitudes of the heavier black hole $a_1$ , the lighter black hole $a_2$ and the final black hole (resulting from the coalescence) $a_\mathrm{f}$ , are slightly narrower. This makes sense, as including the extra imprint from the full effects of precession gives us a bit more information about the spins. The plots below show the constraints on the spins from the two precessing waveforms: the distributions are more condensed with the new results.

Black hole spins estimated using precessing IMRPhenom and EOBNR waveforms

Comparison of orientations and magnitudes of the two component spins. The spin is perfectly aligned with the orbital angular momentum if the angle is 0. The left disk shows results using the precessing IMRPhenom model, the right using the precessing EOBNR model. In each, the distribution for the more massive black hole is on the left, and for the smaller black hole on the right. Adapted from Figure 5 of the Parameter Estimation Paper and Figure 4 of the Precession Paper.

In conclusion, this analysis had shown that included the full effects of precession do give slightly better estimates of the black hole spins. However, it is safe to trust the IMRPhenom results.

If you are looking for the best parameter estimates for GW150914, these results are better than the original results in the Parameter Estimation Paper. However, the O2 Catalogue Paper includes results using improved calibration and noise power spectral density estimation, as well as using precessing waveforms!

The Systematics Paper

Synopsis: Systematics Paper
Read this if: You want to know how parameter estimation could fare for future detections
Favourite part: There’s no need to panic yet

The Precession Paper highlighted how important it is to have good waveform templates. If there is an error in our templates, either because of modelling or because we are missing some physics, then our estimated parameters could be wrong—we would have a source of systematic error.

We know our waveform models aren’t perfect, so there must be some systematic error, the question is how much? From our analysis so far (such as the good agreement between different waveforms in the Precession Paper), we think that systematic error is less significant than the statistical uncertainty which is a consequence of noise in the detectors. In this paper, we try to quantify systematic error for GW150914-like systems.

To asses systematic errors, we analyse waveforms calculated by numerical relativity simulations into data around the time of GW150914. Numerical relativity exactly solves Einstein’s field equations (which govern general relativity), so results of these simulations give the most accurate predictions for the form of gravitational waves. As we know the true parameters for the injected waveforms, we can compare these to the results of our parameter estimation analysis to check for biases.

We use waveforms computed by two different codes: the Spectral Einstein Code (SpEC) and the Bifunctional Adaptive Mesh (BAM) code. (Don’t the names make them sound like such fun?) Most waveforms are injected into noise-free data, so that we know that any offset in estimated parameters is dues to the waveforms and not detector noise; however, we also tried a few injections into real data from around the time of GW150914. The signals are analysed using our standard set-up as used in the Parameter Estimation Paper (a couple of injections are also included in the Precession Paper, where they are analysed with the fully precessing EOBNR waveform to illustrate its accuracy).

The results show that in most cases, systematic errors from our waveform models are small. However, systematic errors can be significant for some orientations of precessing binaries. If we are looking at the orbital plane edge on, then there can be errors in the distance, the mass ratio and the spins, as illustrated below [bonus note]. Thankfully, edge-on binaries are quieter than face-on binaries, and so should make up only a small fraction of detected sources (GW150914 is most probably face off). Furthermore, biases are only significant for some polarization angles (an angle which describes the orientation of the detectors relative to the stretch/squash of the gravitational wave polarizations). Factoring this in, a rough estimate is that about 0.3% of detected signals would fall into the unlucky region where waveform biases are important.

Inclination dependence of parameter recovery

Parameter estimation results for two different GW150914-like numerical relativity waveforms for different inclinations and polarization angles. An inclination of $0^\circ$ means the binary is face on, $180^\circ$ means it face off, and an inclination around $90^\circ$ is edge on. The bands show the recovered 90% credible interval; the dark lines the median values, and the dotted lines show the true values. The (grey) polarization angle $\psi = 82^\circ$ was chosen so that the detectors are approximately insensitive to the $h_+$ polarization. Figure 4 of the Systematics Paper.

While it seems that we don’t have to worry about waveform error for GW150914, this doesn’t mean we can relax. Other systems may show up different aspects of waveform models. For example, our approximants only include the dominant modes (spherical harmonic decompositions of the gravitational waves). Higher-order modes have more of an impact in systems where the two black holes are unequal masses, or where the binary has a higher total mass, so that the merger and ringdown parts of the waveform are more important. We need to continue work on developing improved waveform models (or at least, including our uncertainty about them in our analysis), and remember to check for biases in our results!

The Numerical Relativity Comparison Paper

Synopsis: Numerical Relativity Comparison Paper
Read this if: You are really suspicious of our waveform models, or really like long tables or numerical data
Favourite part: We might one day have enough numerical relativity waveforms to do full parameter estimation with them

In the Precession Paper we discussed how important it was to have accurate waveforms; in the Systematics Paper we analysed numerical relativity waveforms to check the accuracy of our results. Since we do have numerical relativity waveforms, you might be wondering why we don’t just use these in our analysis? In this paper, we give it a go.

Our standard parameter-estimation code (LALInference) randomly hops around parameter space, for each set of parameters we generate a new waveform and see how this matches the data. This is an efficient way of exploring the parameter space. Numerical relativity waveforms are too computationally expensive to generate one each time we hop. We need a different approach.

The alternative, is to use existing waveforms, and see how each of them match. Each simulation gives the gravitational waves for a particular mass ratio and combination of spins, we can scale the waves to examine different total masses, and it is easy to consider what the waves would look like if measured at a different position (distance, inclination or sky location). Therefore, we can actually cover a fair range of possible parameters with a given set of simulations.

To keep things quick, the code averages over positions, this means we don’t currently get an estimate on the redshift, and so all the masses are given as measured in the detector frame and not as the intrinsic masses of the source.

The number of numerical relativity simulations is still quite sparse, so to get nice credible regions, a simple Gaussian fit is used for the likelihood. I’m not convinced that this capture all the detail of the true likelihood, but it should suffice for a broad estimate of the width of the distributions.

The results of this analysis generally agree with those from our standard analysis. This is a relief, but not surprising given all the other checks that we have done! It hints that we might be able to get slightly better measurements of the spins and mass ratios if we used more accurate waveforms in our standard analysis, but the overall conclusions are sound.

I’ve been asked if since these results use numerical relativity waveforms, they are the best to use? My answer is no. As well as potential error from the sparse sampling of simulations, there are several small things to be wary of.

We only have short numerical relativity waveforms. This means that the analysis only goes down to a frequency of $30~\mathrm{Hz}$ and ignores earlier cycles. The standard analysis includes data down to $20~\mathrm{Hz}$ , and this extra data does give you a little information about precession. (The limit of the simulation length also means you shouldn’t expect this type of analysis for the longer LVT151012 or GW151226 any time soon).
This analysis doesn’t include the effects of calibration uncertainty. There is some uncertainty in how to convert from the measured signal at the detectors’ output to the physical strain of the gravitational wave. Our standard analysis fold this in, but that isn’t done here. The estimates of the spin can be affected by miscalibration. (This paper also uses the earlier calibration, rather than the improved calibration of the O1 Binary Black Hole Paper).
Despite numerical relativity simulations producing waveforms which include all higher modes, not all of them are actually used in the analysis. More are included than in the standard analysis, so this will probably make negligible difference.

Finally, I wanted to mention one more detail, as I think it is not widely appreciated. The gravitational wave likelihood is given by an inner product

$\displaystyle L \propto \exp \left[- \int_{-\infty}^{\infty} \mathrm{d}f \frac{|s(f) - h(f)|^2}{S_n(f)} \right]$ ,

where $s(f)$ is the signal, $h(f)$ is our waveform template and $S_n(f)$ is the noise spectral density (PSD). These are the three things we need to know to get the right answer. This paper, together with the Precession Paper and the Systematics Paper, has been looking at error from our waveform models $h(f)$ . Uncertainty from the calibration of $s(f)$ is included in the standard analysis, so we know how to factor this in (and people are currently working on more sophisticated models for calibration error). This leaves the noise PSD $S_n(f)$ …

The noise PSD varies all the time, so it needs to be estimated from the data. If you use a different stretch of data, you’ll get a different estimate, and this will impact your results. Ideally, you would want to estimate from the time span that includes the signal itself, but that’s tricky as there’s a signal in the way. The analysis in this paper calculates the noise power spectral density using a different time span and a different method than our standard analysis; therefore, we expect some small difference in the estimated parameters. This might be comparable to (or even bigger than) the difference from switching waveforms! We see from the similarity of results that this cannot be a big effect, but it means that you shouldn’t obsess over small differences, thinking that they could be due to waveform differences, when they could just come from estimation of the noise PSD.

Lots of work is currently going into making sure that the numerator term $|s(f) - h(f)|^2$ is accurate. I think that the denominator $S_n(f)$ needs attention too. Since we have been kept rather busy, including uncertainty in PSD estimation will have to wait for a future set papers.

Bonus notes

Finches

100 bonus points to anyone who folds up the papers to make beaks suitable for eating different foods.

The right answer

Our current best estimate for the chirp mass (from the O2 Catalogue Paper) would be $31.2_{-1.5}^{+1.7} M_\odot$ . You need proper templates for the gravitational wave signal to calculate this. If you factor in the the gravitational wave gets redshifted (shifted to lower frequency by the expansion of the Universe), then the true chirp mass of the source system is $28.6_{-1.5}^{+1.6} M_\odot$ .

Formative experiences

My one undergraduate lecture on gravitational waves was the penultimate lecture of the fourth-year general relativity course. I missed this lecture, as I had a PhD interview (at the University of Birmingham). Perhaps if I had sat through it, my research career would have been different?

Good things come…

The computational expense of a waveform is important, as when we are doing parameter estimation, we calculate lots (tens of millions) of waveforms for different parameters to see how they match the data. Before O1, the task of using SEOBNRv3 for parameter estimation seemed quixotic. The first detection, however, was enticing enough to give it a try. It was a truly heroic effort by Vivien Raymond and team that produced these results—I am slightly suspicious the Vivien might actually be a wizard.

GW150914 is a short signal, meaning it is relatively quick to analyse. Still, it required us using all the tricks at our disposal to get results in a reasonable time. When it came time to submit final results for the Discovery Paper, we had just about 1,000 samples from the posterior probability distribution for the precessing EOBNR waveform. For comparison, we had over 45,000 sample for the non-precessing EOBNR waveform. 1,000 samples isn’t enough to accurately map out the probability distributions, so we decided to wait and collect more samples. The preliminary results showed that things looked similar, so there wouldn’t be a big difference in the science we could do. For the Precession Paper, we finally collected 2,700 samples. This is still a relatively small number, so we carefully checked the uncertainty in our results due to the finite number of samples.

The Precession Paper has shown that it is possible to use the precessing EOBNR for parameter estimation, but don’t expect it to become the norm, at least until we have a faster implementation of it. Vivien is only human, and I’m sure his family would like to see him occasionally.

Parameter key

In case you are wondering what all the symbols in the results plots stand for, here are their usual definitions. First up, the various masses

$m_1$ —the mass of the heavier black hole, sometimes called the primary black hole;
$m_2$ —the mass of the lighter black hole, sometimes called the secondary black hole;
$M$ —the total mass of the binary, $M = m_1 + m_2$ ;
$M_\mathrm{f}$ —the mass of the final black hole (after merger);
$\mathcal{M}$ —the chirp mass, the combination of the two component masses which sets how the binary inspirals together;
$q$ —the mass ratio, $q = m_1/m_2 \leq 1$ . Confusingly, numerical relativists often use the opposite convention $q = m_2/m_1 \geq 1$ (which is why the Numerical Relativity Comparison Paper discusses results in terms of $1/q$ : we can keep the standard definition, but all the numbers are numerical relativist friendly).

A superscript “source” is sometimes used to distinguish the actual physical masses of the source from those measured by the detector which have been affected by cosmological redshift. The measured detector-frame mass is $m = (1 + z) m^\mathrm{source}$ , where $m^\mathrm{source}$ is the true, redshift-corrected source-frame mass and $z$ is the redshift. The mass ratio $q$ is independent of the redshift. On the topic of redshift, we have

$z$ —the cosmological redshift ( $z = 0$ would be now);
$D_\mathrm{L}$ —the luminosity distance.

The luminosity distance sets the amplitude of the signal, as does the orientation which we often describe using

$\iota$ —the inclination, the angle between the line of sight and the orbital angular momentum ( $\boldsymbol{L}$ ). This is zero for a face-on binary.
$\theta_{JN}$ —the angle between the line of sight ( $\boldsymbol{N}$ ) and the total angular momentum of the binary ( $\boldsymbol{J}$ ); this is approximately equal to the inclination, but is easier to use for precessing binaries.

As well as masses, black holes have spins

$a_1$ —the (dimensionless) spin magnitude of the heavier black hole, which is between $0$ (no spin) and $1$ (maximum spin);
$a_2$ —the (dimensionless) spin magnitude of the lighter black hole;
$a_\mathrm{f}$ —the (dimensionless) spin magnitude of the final black hole;
$\chi_\mathrm{eff}$ —the effective inspiral spin parameter, a combinations of the two component spins which has the largest impact on the rate of inspiral (think of it as the spin equivalent of the chirp mass);
$\chi_\mathrm{p}$ —the effective precession spin parameter, a combination of spins which indicate the dominant effects of precession, it’s $0$ for no precession and $1$ for maximal precession;
$\theta_{LS_1}$ —the primary tilt angle, the angle between the orbital angular momentum and the heavier black holes spin ( $\boldsymbol{S_1}$ ). This is zero for aligned spin.
$\theta_{LS_2}$ —the secondary tilt angle, the angle between the orbital angular momentum and the lighter black holes spin ( $\boldsymbol{S_2}$ ).
$\phi_{12}$ —the angle between the projections of the two spins on the orbital plane.

The orientation angles change in precessing binaries (when the spins are not perfectly aligned or antialigned with the orbital angular momentum), so we quote values at a reference time corresponding to when the gravitational wave frequency is $20~\mathrm{Hz}$ . Finally (for the plots shown here)

$\psi$ —the polarization angle, this is zero when the detector arms are parallel to the $h_+$ polarization’s stretch/squash axis.

For more detailed definitions, check out the Parameter Estimation Paper or the LALInference Paper.

Going the distance: Mapping host galaxies of LIGO and Virgo sources in three dimensions using local cosmography and targeted follow-up

October 22, 2016August 10, 2018 / CPLB / Leave a comment

GW150914 claimed the title of many firsts—it was the first direct observation of gravitational waves, the first observation of a binary black hole system, the first observation of two black holes merging, the first time time we’ve tested general relativity in such extreme conditions… However, there are still many firsts for gravitational-wave astronomy yet to come (hopefully, some to be accompanied by cake). One of the most sought after, is the first is signal to have a clear electromagnetic counterpart—a glow in some part of the spectrum of light (from radio to gamma-rays) that we can observe with telescopes.

Identifying a counterpart is challenging, as it is difficult to accurately localise a gravitational-wave source. electromagnetic observers must cover a large area of sky before any counterparts fade. Then, if something is found, it can be hard to determine if that is from the same source as the gravitational waves, or some thing else…

To help the search, it helps to have as much information as possible about the source. Especially useful is the distance to the source. This can help you plan where to look. For nearby sources, you can cross-reference with galaxy catalogues, and perhaps pick out the biggest galaxies as the most likely locations for the source [bonus note]. Distance can also help plan your observations: you might want to start with regions of the sky where the source would be closer and so easiest to spot, or you may want to prioritise points where it is further and so you’d need to observe longer to detect it (I’m not sure there’s a best strategy, it depends on the telescope and the amount of observing time available). In this paper we describe a method to provide easy-to-use distance information, which could be supplied to observers to help their search for a counterpart.

Going the distance

This work is the first spin-off from the First 2 Years trilogy of papers, which looked a sky localization and parameter estimation for binary neutron stars in the first two observing runs of the advance-detector era. Binary neutron star coalescences are prime candidates for electromagnetic counterparts as we think there should be a bigger an explosion as they merge. I was heavily involved in the last two papers of the trilogy, but this study was led by Leo Singer: I think I mostly annoyed Leo by being a stickler when it came to writing up the results.

3D localization with the two LIGO detectors

Three-dimensional localization showing the 20%, 50%, and 90% credible levels for a typical two-detector early Advanced LIGO event. The Earth is shown at the centre, marked by $\oplus$ . The true location is marked by the cross. Leo poetically described this as looking like the seeds of the jacaranda tree, and less poetically as potato chips. Figure 1 of Singer et al. (2016).

The idea is to provide a convenient means of sharing a 3D localization for a gravitational wave source. The full probability distribution is rather complicated, but it can be made more manageable if you break it up into pixels on the sky. Since astronomers need to decide where to point their telescopes, breaking up the 3D information along different lines of sight, should be useful for them.

Each pixel covers a small region of the sky, and along each line of sight, the probability distribution for distance $D$ can be approximated using an ansatz

$\displaystyle p(D|\mathrm{data}) \propto D^2\exp\left[-\frac{(D - \mu)^2}{2\sigma}\right]$ ,

where $\mu$ and $\sigma$ are calculated for each pixel individually. The form of this ansatz can be understood as the posterior probability distribution is proportional to the product of the prior and the likelihood. Our prior is that sources are uniformly distributed in volume, which means $\propto D^2$ , and the likelihood can often be well approximated as a Gaussian distribution, which gives the other piece [bonus note].

The ansatz doesn’t always fit perfectly, but it performs well on average. Considering the catalogue of binary neutron star signals used in the earlier papers, we find that roughly 50% of the time sources are found within the 50% credible volume, 90% are found in the 90% volume, etc. We looked at a more sophisticated means of constructing the localization volume in a companion paper.

The 3D localization is easy to calculate, and Leo has worked out a cunning way to evaluate the ansatz with BAYESTAR, our rapid sky-localization code, meaning that we can produce it on minute time-scales. This means that observers should have something to work with straight-away, even if we’ll need to wait a while for the full, final results. We hope that this will improve prospects for finding counterparts—some potential examples are sketched out in the penultimate section of the paper.

If you are interested in trying out the 3D information, there is a data release and the supplement contains a handy Python tutorial. We are hoping that the Collaboration will use the format for alerts for LIGO and Virgo’s upcoming observing run (O2).

arXiv: 1603.07333 [astro-ph.HE]; 1605.04242 [astro-ph.IM]
Journal: Astrophysical Journal Letters; 829(1):L15(7); 2016; Astrophysical Journal Supplement Series; 226(1):10(8); 2016
Data release: Going the distance
Favourite crisp flavour: Salt & vinegar
Favourite jacaranda: Jacaranda mimosifolia

Bonus notes

Catalogue shopping

The Event’s source has a luminosity distance of around 250–570 Mpc. This is sufficiently distant that galaxy catalogues are incomplete and not much use when it comes to searching. GW151226 and LVT151012 have similar problems, being at around the same distance or even further.

The gravitational-wave likelihood

For the professionals interested in understanding more about the shape of the likelihood, I’d recommend Cutler & Flanagan (1994). This is a fantastic paper which contains many clever things [bonus bonus note]. This work is really the foundation of gravitational-wave parameter estimation. From it, you can see how the likelihood can be approximated as a Gaussian. The uncertainty can then be evaluated using Fisher matrices. Many studies have been done using Fisher matrices, but it important to check that this is a valid approximation, as nicely explained in Vallisneri (2008). I ran into a case when it didn’t during my PhD.

Mergin’

As a reminder that smart people make mistakes, Cutler & Flanagan have a typo in the title of arXiv posting of their paper. This is probably the most important thing to take away from this paper.

Parameter estimation on gravitational waves from neutron-star binaries with spinning components

October 1, 2016October 15, 2017 / CPLB / Leave a comment

blIn gravitation-wave astronomy, some parameters are easier to measure than others. We are sensitive to properties which change the form of the wave, but sometimes the effect of changing one parameter can be compensated by changing another. We call this a degeneracy. In signals for coalescing binaries (two black holes or neutron stars inspiralling together), there is a degeneracy between between the masses and spins. In this recently published paper, we look at what this means for observing binary neutron star systems.

History

This paper has been something of an albatross, and I’m extremely pleased that we finally got it published. I started working on it when I began my post-doc at Birmingham in 2013. Back then I was sharing an office with Ben Farr, and together with others in the Parameter Estimation Group, we were thinking about the prospect of observing binary neutron star signals (which we naively thought were the most likely) in LIGO’s first observing run.

One reason that this work took so long is that binary neutron star signals can be computationally expensive to analyse [bonus note]. The signal slowly chirps up in frequency, and can take up to a minute to sweep through the range of frequencies LIGO is sensitive to. That gives us a lot of gravitational wave to analyse. (For comparison, GW150914 lasted 0.2 seconds). We need to calculate waveforms to match to the observed signals, and these can be especially complicated when accounting for the effects of spin.

A second reason is shortly after submitting the paper in August 2015, we got a little distracted…

This paper was the third of a trilogy look at measuring the properties of binary neutron stars. I’ve written about the previous instalment before. We knew that getting the final results for binary neutron stars, including all the important effects like spin, would take a long time, so we planned to follow up any detections in stages. A probable sky location can be computed quickly, then we can have a first try at estimating other parameters like masses using waveforms that don’t include spin, then we go for the full results with spin. The quicker results would be useful for astronomers trying to find any explosions that coincided with the merger of the two neutron stars. The first two papers looked at results from the quicker analyses (especially at sky localization); in this one we check what effect neglecting spin has on measurements.

What we did

We analysed a population of 250 binary neutron star signals (these are the same as the ones used in the first paper of the trilogy). We used what was our best guess for the sensitivity of the two LIGO detectors in the first observing run (which was about right).

The simulated neutron stars all have small spins of less than 0.05 (where 0 is no spin, and 1 would be the maximum spin of a black hole). We expect neutron stars in these binaries to have spins of about this range. The maximum observed spin (for a neutron star not in a binary neutron star system) is around 0.4, and we think neutron stars should break apart for spins of 0.7. However, since we want to keep an open mind regarding neutron stars, when measuring spins we considered spins all the way up to 1.

What we found

Our results clearly showed the effect of the mass–spin degeneracy. The degeneracy increases the uncertainty for both the spins and the masses.

Even though the true spins are low, we find that across the 250 events, the median 90% upper limit on the spin of the more massive (primary) neutron star is 0.70, and the 90% limit on the less massive (secondary) neutron star is 0.86. We learn practically nothing about the spin of the secondary, but a little more about the spin of the primary, which is more important for the inspiral. Measuring spins is hard.

The effect of the mass–spin degeneracy for mass measurements is shown in the plot below. Here we show a random selection of events. The banana-shaped curves are the 90% probability intervals. They are narrow because we can measure a particular combination of masses, the chirp mass, really well. The mass–spin degeneracy determines how long the banana is. If we restrict the range of spins, we explore less of the banana (and potentially introduce an offset in our results).

Rough outlines for 90% credible regions for component masses for a random assortments of signals. The circles show the true values. The coloured lines indicate the extent of the distribution with different limits on the spins. The grey area is excluded from our convention on masses $m_1 \geq m_2$ . Figure 5 from Farr et al. (2016).

Although you can’t see it in the plot above, including spin does also increase the uncertainty in the chirp mass too. The plots below show the standard deviation (a measure width of the posterior probability distribution), divided by the mean for several mass parameters. This gives a measure of the fractional uncertainty in our measurements. We show the chirp mass $\mathcal{M}_\mathrm{c}$ , the mass ratio $q = m_2/m_1$ and the total mass $M = m_1 + m_2$ , where $m_1$ and $m_2$ are the masses of the primary and secondary neutron stars respectively. The uncertainties are small for louder signals (higher signal-to-noise ratio). If we neglect the spin, the true chirp mass can lie outside the posterior distribution, the average is about 5 standard deviations from the mean, but if we include spin, the offset is just 0.7 from the mean (there’s still some offset as we’re allowing for spins all the way up to 1).

Mass measurements for binary neutron stars with and without spin

Fractional statistical uncertainties in chirp mass (top), mass ratio (middle) and total mass (bottom) estimates as a function of network signal-to-noise ratio for both the fully spinning analysis and the quicker non-spinning analysis. The lines indicate approximate power-law trends to guide the eye. Figure 2 of Farr et al. (2016).

We need to allow for spins when measuring binary neutron star masses in order to explore for the possible range of masses.

Sky localization and distance, however, are not affected by the spins here. This might not be the case for sources which are more rapidly spinning, but assuming that binary neutron stars do have low spin, we are safe using the easier-to-calculate results. This is good news for astronomers who need to know promptly where to look for explosions.

arXiv: 1508.05336 [astro-ph.HE]
Journal: Astrophysical Journal; 825(2):116(10); 2016
Authorea [bonus note]: Parameter estimation on gravitational waves from neutron-star binaries with spinning components
Conference proceedings: Early Advanced LIGO binary neutron-star sky localization and parameter estimation
Favourite albatross: Wilbur

Bonus notes

How long?

The plot below shows how long it took to analyse each of the binary neutron star signals.

Run time for different analyses of binary neutron stars

Distribution of run times for binary neutron star signals. Low-latency sky localization is done with BAYESTAR; medium-latency non-spinning parameter estimation is done with LALInference and TaylorF2 waveforms, and high-latency fully spinning parameter estimation is done with LALInference and SpinTaylorT4 waveforms. The LALInference results are for 2000 posterior samples. Figure 9 from Farr et al. (2016).

BAYESTAR provides a rapid sky localization, taking less than ten seconds. This is handy for astronomers who want to catch a flash caused by the merger before it fades.

Estimates for the other parameters are computed with LALInference. How long this takes to run depends on which waveform you are using and how many samples from the posterior probability distribution you want (the more you have, the better you can map out the shape of the distribution). Here we show times for 2000 samples, which is enough to get a rough idea (we collected ten times more for GW150914 and friends). Collecting twice as many samples takes (roughly) twice as long. Prompt results can be obtained with a waveform that doesn’t include spin (TaylorF2), these take about a day at most.

For this work, we considered results using a waveform which included the full effects of spin (SpinTaylorT4). These take about twenty times longer than the non-spinning analyses. The maximum time was 172 days. I have a strong suspicion that the computing time cost more than my salary.

Waiting for LALInference runs to finish gives you some time to practise hobbies. This is a globe knitted by Hannah. The two LIGO sites marked in red, and a typical gravitational-wave sky localization stitched on.

In order to get these results, we had to add check-pointing to our code, so we could stop it and restart it; we encountered a new type of error in the software which manages jobs running on our clusters, and Hannah Middleton and I got several angry emails from cluster admins (who are wonderful people) for having too many jobs running.

In comparison, analysing GW150914, LVT151012 and GW151226 was a breeze. Grudgingly, I have to admit that getting everything sorted out for this study made us reasonably well prepared for the real thing. Although, I’m not looking forward to that first binary neutron star signal…

Authorea

Authorea is an online collaborative writing service. It allows people to work together on documents, editing text, adding comments, and chatting with each other. By the time we came to write up the paper, Ben was no longer in Birmingham, and many of our coauthors are scattered across the globe. Ben thought Authorea might be useful for putting together the paper.

Writing was easy, and the ability to add comments on the text was handy for getting feedback from coauthors. The chat was going for quickly sorting out issues like plots. Overall, I was quite pleased, up to the point we wanted to get the final document. Extracted a nicely formatted PDF was awkward. For this I switched to using the Github back-end. On reflection, a simple git repo, plus a couple of Skype calls might have been a smoother way of writing, at least for a standard journal article.

Authorea promises to be an open way of producing documents, and allows for others to comment on papers. I don’t know if anyone’s looked at our Authorea article. For astrophysics, most people use the arXiv, which is free to everyone, and I’m not sure if there’s enough appetite for interaction (beyond the occasional email to authors) to motivate people to look elsewhere. At least, not yet.

In conclusion, I think Authorea is a nice idea, and I would try out similar collaborative online writing tools again, but I don’t think I can give it a strong recommendation for your next paper unless you have a particular idea in mind of how to make the most of it.

Testing general relativity using golden black-hole binaries

August 27, 2016October 15, 2017 / CPLB / Leave a comment

Binary black hole mergers are the ultimate laboratory for testing gravity. The gravitational fields are strong, and things are moving at close to the speed of light. these extreme conditions are exactly where we expect our theories could breakdown, which is why we were so exciting by detecting gravitational waves from black hole coalescences. To accompany the first detection of gravitational waves, we performed several tests of Einstein’s theory of general relativity (it passed). This paper outlines the details of one of the tests, one that can be extended to include future detections to put Einstein’s theory to the toughest scrutiny.

One of the difficulties of testing general relativity is what do you compare it to? There are many alternative theories of gravity, but only a few of these have been studied thoroughly enough to give an concrete idea of what a binary black hole merger should look like. Even if general relativity comes out on top when compared to one alternative model, it doesn’t mean that another (perhaps one we’ve not thought of yet) can be ruled out. We need ways of looking for something odd, something which hints that general relativity is wrong, but doesn’t rely on any particular alternative theory of gravity.

The test suggested here is a consistency test. We split the gravitational-wave signal into two pieces, a low frequency part and a high frequency part, and then try to measure the properties of the source from the two parts. If general relativity is correct, we should get answers that agree; if it’s not, and there’s some deviation in the exact shape of the signal at different frequencies, we can get different answers. One way of thinking about this test is imagining that we have two experiments, one where we measure lower frequency gravitational waves and one where we measure higher frequencies, and we are checking to see if their results agree.

To split the waveform, we use a frequency around that of the last stable circular orbit: about the point that the black holes stop orbiting about each other and plunge together and merge [bonus note]. For GW150914, we used 132 Hz, which is about the same as the C an octave below middle C (a little before time zero in the simulation below). This cut roughly splits the waveform into the low frequency inspiral (where the two black hole are orbiting each other), and the higher frequency merger (where the two black holes become one) and ringdown (where the final black hole settles down).

We are fairly confident that we understand what goes on during the inspiral. This is similar physics to where we’ve been testing gravity before, for example by studying the orbits of the planets in the Solar System. The merger and ringdown are more uncertain, as we’ve never before probed these strong and rapidly changing gravitational fields. It therefore seems like a good idea to check the two independently [bonus note].

We use our parameter estimation codes on the two pieces to infer the properties of the source, and we compare the values for the mass $M_f$ and spin $\chi_f$ of the final black hole. We could use other sets of parameters, but this pair compactly sum up the properties of the final black hole and are easy to explain. We look at the difference between the estimated values for the mass and spin, $\Delta M_f$ and $\Delta \chi_f$ , if general relativity is a good match to the observations, then we expect everything to match up, and $\Delta M_f$ and $\Delta \chi_f$ to be consistent with zero. They won’t be exactly zero because we have noise in the detector, but hopefully zero will be within the uncertainty region [bonus note]. An illustration of the test is shown below, including one of the tests we did to show that it does spot when general relativity is not correct.

Results from the consistency test. The top panels show the outlines of the 50% and 90% credible levels for the low frequency (inspiral) part of the waveform, the high frequency (merger–ringdown) part, and the entire (inspiral–merger–ringdown, IMR) waveform. The bottom panel shows the fractional difference between the high and low frequency results. If general relativity is correct, we expect the distribution to be consistent with $(0,0)$ , indicated by the cross (+). The left panels show a general relativity simulation, and the right panel shows a waveform from a modified theory of gravity. Figure 1 of Ghosh et al. (2016).

A convenient feature of using $\Delta M_f$ and $\Delta \chi_f$ to test agreement with relativity, is that you can combine results from multiple observations. By averaging over lots of signals, you can reduce the uncertainty from noise. This allows you to pin down whether or not things really are consistent, and spot smaller deviations (we could get precision of a few percent after about 100 suitable detections). I look forward to seeing how this test performs in the future!

arXiv: 1602.02453 [gr-qc]
Journal: Physical Review D; 94(2):021101(6); 2016
Favourite golden thing: Golden syrup sponge pudding

Bonus notes

Review

I became involved in this work as a reviewer. The LIGO Scientific Collaboration is a bit of a stickler when it comes to checking its science. We had to check that the test was coded up correctly, that the results made sense, and that calculations done and written up for GW150914 were all correct. Since most of the team are based in India [bonus note], this involved some early morning telecons, but it all went smoothly.

One of our checks was that the test wasn’t sensitive to exact frequency used to split the signal. If you change the frequency cut, the results from the two sections do change. If you lower the frequency, then there’s less of the low frequency signal and the measurement uncertainties from this piece get bigger. Conversely, there’ll be more signal in the high frequency part and so we’ll make a more precise measurement of the parameters from this piece. However, the overall results where you combine the two pieces stay about the same. You get best results when there’s a roughly equal balance between the two pieces, but you don’t have to worry about getting the cut exactly on the innermost stable orbit.

Golden binaries

In order for the test to work, we need the two pieces of the waveform to both be loud enough to allow us to measure parameters using them. This type of signals are referred to as golden. Earlier work on tests of general relativity using golden binaries has been done by Hughes & Menou (2015), and Nakano, Tanaka & Nakamura (2015). GW150914 was a golden binary, but GW151226 and LVT151012 were not, which is why we didn’t repeat this test for them.

GW150914 results

For The Event, we ran this test, and the results are consistent with general relativity being correct. The plots below show the estimates for the final mass and spin (here denoted $a_f$ rather than $\chi_f$ ), and the fractional difference between the two measurements. The points $(0,0)$ is at the 28% credible level. This means that if general relativity is correct, we’d expect a deviation at this level to occur around-about 72% of the time due to noise fluctuations. It wouldn’t take a particular rare realisation of noise to cause the assume true value of $(0,0)$ to be found at this probability level, so we’re not too suspicious that something is amiss with general relativity.

Results from the consistency test for The Event. The top panels final mass and spin measurements from the low frequency (inspiral) part of the waveform, the high frequency (post-inspiral) part, and the entire (IMR) waveform. The bottom panel shows the fractional difference between the high and low frequency results. If general relativity is correct, we expect the distribution to be consistent with $(0,0)$ , indicated by the cross. Figure 3 of the Testing General Relativity Paper.

The authors

Abhirup Ghosh and Archisman Ghosh were two of the leads of this study. They are both A. Ghosh at the same institution, which caused some confusion when compiling the LIGO Scientific Collaboration author list. I think at one point one of them (they can argue which) was removed as someone thought there was a mistaken duplication. To avoid confusion, they now have their full names used. This is a rare distinction on the Discovery Paper (I’ve spotted just two others). The academic tradition of using first initials plus second name is poorly adapted to names which don’t fit the typical western template, so we should be more flexible.

Inference on gravitational waves from coalescences of stellar-mass compact objects and intermediate-mass black holes

June 4, 2016August 27, 2016 / CPLB / Leave a comment

I love collecting things, there’s something extremely satisfying about completing a set. I suspect that this is one of the alluring features of Pokémon—you’ve gotta catch ’em all. The same is true of black hole hunting. Currently, we know of stellar-mass black holes which are a few times the mass of our Sun, up to a few tens of the mass of our Sun (the black holes of GW150914 are the biggest yet to be observed), and we know of supermassive black holes, which are ten thousand to ten billion times the mass our Sun. However, we are missing intermediate-mass black holes which lie in the middle. We have Charmander and Charizard, but where is Charmeleon? The elusive ones are always the most satisfying to capture.

Adorable black hole (available for adoption). I’m sure this could be a Pokémon. It would be a Dark type. Not that I’ve given it that much thought…

Intermediate-mass black holes have evaded us so far. We’re not even sure that they exist, although that would raise questions about how you end up with the supermassive ones (you can’t just feed the stellar-mass ones lots of rare candy). Astronomers have suggested that you could spot intermediate-mass black holes in globular clusters by the impact of their gravity on the motion of other stars. However, this effect would be small, and near impossible to conclusively spot. Another way (which I’ve discussed before), would to be to look at ultra luminous X-ray sources, which could be from a disc of material spiralling into the black hole. However, it’s difficult to be certain that we understand the source properly and that we’re not misclassifying it. There could be one sure-fire way of identifying intermediate-mass black holes: gravitational waves.

The frequency of gravitational waves depend upon the mass of the binary. More massive systems produce lower frequencies. LIGO is sensitive to the right range of frequencies for stellar-mass black holes. GW150914 chirped up to the pitch of a guitar’s open B string (just below middle C). Supermassive black holes produce gravitational waves at too low frequency for LIGO (a space-based detector would be perfect for these). We might just be able to detect signals from intermediate-mass black holes with LIGO.

In a recent paper, a group of us from Birmingham looked at what we could learn from gravitational waves from the coalescence of an intermediate-mass black hole and a stellar-mass black hole [bonus note]. We considered how well you would be able to measure the masses of the black holes. After all, to confirm that you’ve found an intermediate-mass black hole, you need to be sure of its mass.

The signals are extremely short: we only can detect the last bit of the two black holes merging together and settling down as a final black hole. Therefore, you might think there’s not much information in the signal, and we won’t be able to measure the properties of the source. We found that this isn’t the case!

We considered a set of simulated signals, and analysed these with our parameter-estimation code [bonus note]. Below are a couple of plots showing the accuracy to which we can infer a couple of different mass parameters for binaries of different masses. We show the accuracy of measuring the chirp mass $\mathcal{M}$ (a much beloved combination of the two component masses which we are usually able to pin down precisely) and the total mass $M_\mathrm{total}$ .

Measured chirp mass for systems of different total masses. The shaded regions show the 90% credible interval and the dashed lines show the true values. The mass ratio $q$ is the mass of the stellar-mass black hole divided by the mass of the intermediate-mass black hole. Figure 1 of Haster et al. (2016).

Measured total mass for systems of different total masses. The shaded regions show the 90% credible interval and the dashed lines show the true values. Figure 2 of Haster et al. (2016).

For the lower mass systems, we can measure the chirp mass quite well. This is because we get a little information from the part of the gravitational wave from when the two components are inspiralling together. However, we see less and less of this as the mass increases, and we become more and more uncertain of the chirp mass.

The total mass isn’t as accurately measured as the chirp mass at low masses, but we see that the accuracy doesn’t degrade at higher masses. This is because we get some constraints on its value from the post-inspiral part of the waveform.

We found that the transition from having better fractional accuracy on the chirp mass to having better fractional accuracy on the total mass happened when the total mass was around 200–250 solar masses. This was assuming final design sensitivity for Advanced LIGO. We currently don’t have as good sensitivity at low frequencies, so the transition will happen at lower masses: GW150914 is actually in this transition regime (the chirp mass is measured a little better).

Given our uncertainty on the masses, when can we conclude that there is an intermediate-mass black hole? If we classify black holes with masses more than 100 solar masses as intermediate mass, then we’ll be able to say to claim a discovery with 95% probability if the source has a black hole of at least 130 solar masses. The plot below shows our inferred probability of there being an intermediate-mass black hole as we increase the black hole’s mass (there’s little chance of falsely identifying a lower mass black hole).

Intermediate-mass black hole probability

Probability that the larger black hole is over 100 solar masses (our cut-off mass for intermediate-mass black holes $M_\mathrm{IMBH}$ ). Figure 7 of Haster et al. (2016).

Gravitational-wave observations could lead to a concrete detection of intermediate mass black holes if they exist and merge with another black hole. However, LIGO’s low frequency sensitivity is important for detecting these signals. If detector commissioning goes to plan and we are lucky enough to detect such a signal, we’ll finally be able to complete our set of black holes.

arXiv: 1511.01431 [astro-ph.HE]
Journal: Monthly Notices of the Royal Astronomical Society; 457(4):4499–4506; 2016
Birmingham science summary: Inference on gravitational waves from coalescences of stellar-mass compact objects and intermediate-mass black holes (by Carl)
Other collectables: Breakthrough, Gruber, Shaw, Kavli, …

Bonus notes

Jargon

The coalescence of an intermediate-mass black hole and a stellar-mass object (black hole or neutron star) has typically been known as an intermediate mass-ratio inspiral (an IMRI). This is similar to the name for the coalescence of a a supermassive black hole and a stellar-mass object: an extreme mass-ratio inspiral (an EMRI). However, my colleague Ilya has pointed out that with LIGO we don’t really see much of the intermediate-mass black hole and the stellar-mass black hole inspiralling together, instead we see the merger and ringdown of the final black hole. Therefore, he prefers the name intermediate mass-ratio coalescence (or IMRAC). It’s a better description of the signal we measure, but the acronym isn’t as good.

Parameter-estimation runs

The main parameter-estimation analysis for this paper was done by Zhilu, a summer student. This is notable for two reasons. First, it shows that useful research can come out of a summer project. Second, our parameter-estimation code installed and ran so smoothly that even an undergrad with no previous experience could get some useful results. This made us optimistic that everything would work perfectly in the upcoming observing run (O1). Unfortunately, a few improvements were made to the code before then, and we were back to the usual level of fun in time for The Event.

Prospects for observing and localizing gravitational-wave transients with Advanced LIGO and Advanced Virgo

March 5, 2016June 16, 2018 / CPLB / Leave a comment

The week beginning February 8th was a big one for the LIGO and Virgo Collaborations. You might remember something about a few papers on the merger of a couple of black holes; however, those weren’t the only papers we published that week. In fact, they are not even (currently) the most cited…

Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO and Advanced Virgo is known within the Collaboration as the Observing Scenarios Document. It has a couple of interesting aspects

Its content is a mix of a schedule for detector commissioning and an explanation of data analysis. It is a rare paper that spans both the instrumental and data-analysis sides of the Collaboration.
It is a living review: it is intended to be periodically updated as we get new information.

There is also one further point of interest for me: I was heavily involved in producing this latest version.

In this post I’m going to give an outline of the paper’s content, but delve a little deeper into the story of how this paper made it to print.

The Observing Scenarios

The paper is divided up into four sections.

It opens, as is traditional, with the introduction. This has no mentions of windows, which is a good start.
Section 2 is the instrumental bit. Here we give a possible timeline for the commissioning of the LIGO and Virgo detectors and a plausible schedule for our observing runs.
Next we talk about data analysis for transient (short) gravitational waves. We discuss detection and then sky localization.
Finally, we bring everything together to give an estimate of how well we expect to be able to locate the sources of gravitational-wave signals as time goes on.

Packaged up, the paper is useful if you want to know when LIGO and Virgo might be observing or if you want to know how we locate the source of a signal on the sky. The aim was to provide a guide for those interested in multimessenger astronomy—astronomy where you rely on multiple types of signals like electromagnetic radiation (light, radio, X-rays, etc.), gravitational waves, neutrinos or cosmic rays.

The development of the detectors’ sensitivity is shown below. It takes many years of tweaking and optimising to reach design sensitivity, but we don’t wait until then to do some science. It’s just as important to practise running the instruments and analysing the data as it is to improve the sensitivity. Therefore, we have a series of observing runs at progressively higher sensitivity. Our first observing run (O1), featured just the two LIGO detectors, which were towards the better end of the expected sensitivity.

Plausible evolution of the Advanced LIGO and Advanced Virgo detectors with time. The lower the sensitivity curve, the further away we can detect sources. The distances quoted are ranges we could observe binary neutrons stars (BNSs) to. The BNS-optimized curve is a proposal to tweak the detectors for finding BNSs. Fig. 1 of the Observing Scenarios Document.

It’s difficult to predict exactly how the detectors will progress (we’re doing many things for the first time ever), but the plot above shows our current best plan.

I’ll not go into any more details about the science in the paper as I’ve already used up my best ideas writing the LIGO science summary.

If you’re particularly interested in sky localization, you might like to check out the data releases for studies using (simulated) binary neutron star and burst signals. The binary neutron star analysis is similar to that we do for any compact binary coalescence (the merger of a binary containing neutron stars or black holes), and the burst analysis works more generally as it doesn’t require a template for the expected signal.

The path to publication

Now, this is the story of how a Collaboration paper got published. I’d like to take a minute to tell you how I became responsible for updating the Observing Scenarios…

In the beginning

The Observing Scenarios has its origins long before I joined the Collaboration. The first version of the document I can find is from July 2012. Amongst the labyrinth of internal wiki pages we have, the earliest reference I’ve uncovered was from August 2012 (the plan was to have a mature draft by September). The aim was to give a road map for the advanced-detector era, so the wider astronomical community would know what to expect.

I imagine it took a huge effort to bring together all the necessary experts from across the Collaboration to sit down and write the document.

Any document detailing our plans would need to be updated regularly as we get a better understanding of our progress on commissioning the detectors (and perhaps understanding what signals we will see). Fortunately, there is a journal that can cope with just that: Living Reviews in Relativity. Living Reviews is designed so that authors can update their articles so that they never become (too) out-of-date.

A version was submitted to Living Reviews early in 2013, around the same time as a version was posted to the arXiv. We had referee reports (from two referees), and were preparing to resubmit. Unfortunately, Living Reviews suspended operations before we could. However, work continued.

Updating sky localization

I joined the LIGO Scientific Collaboration when I started at the University of Birmingham in October 2013. I soon became involved in a variety of activities of the Parameter Estimation group (my boss, Alberto Vecchio, is the chair of the group).

Sky localization was a particularly active area as we prepared for the first runs of Advanced LIGO. The original version of the Observing Scenarios Document used a simple approximate means of estimating sky localization, using just timing triangulation (it didn’t even give numbers for when we only had two detectors running). We knew we could do better.

We had all the code developed, but we needed numbers for a realistic population of signals. I was one of the people who helped running the analyses to get these. We had the results by the summer of 2014; we now needed someone to write up the results. I have a distinct recollection of there being silence on our weekly teleconference. Then Alberto asked me if I would do it? I said yes: it would probably only take me a week or two to write a short technical note.

Saying yes is a slippery slope.

That note became Parameter estimation for binary neutron-star coalescences with realistic noise during the Advanced LIGO era, a 24-page paper (it considers more than just sky localization).

Numbers in hand, it was time to update the Observing Scenarios. Even if things were currently on hold with Living Reviews, we could still update the arXiv version. I thought it would be easiest if I put them in, with a little explanation, myself. I compiled a draft and circulated in the Parameter Estimation group. Then it was time to present to the Data Analysis Council.

The Data Analysis Council either sounds like a shadowy organisation orchestrating things from behind the scene, or a place where people bicker over trivial technical issues. In reality it is a little of both. This is the body that should coordinate all the various bits of analysis done by the Collaboration, and they have responsibility for the Observing Scenarios Document. I presented my update on the last call before Christmas 2014. They were generally happy, but said that the sky localization on the burst side needed updating too! There was once again a silence on the call when it came to the question of who would finish off the document. The Observing Scenarios became my responsibility.

(I had though that if I helped out with this Collaboration paper, I could take the next 900 off. This hasn’t worked out.)

The review

With some help from the Burst group (in particular Reed Essick, who had lead their sky localization study), I soon had a new version with fully up-to-date sky localization. This was ready for our March Collaboration meeting. I didn’t go (I was saving my travel budget for the summer), so Alberto presented on my behalf. It was now agreed that the document should go through internal review.

It’s this which I really want to write about. Peer review is central to modern science. New results are always discussed by experts in the community, to try to understand the value of the work; however, peer review is formalised in the refereeing of journal articles, when one or more (usually anonymous) experts examine work before it can be published. There are many ups and down with this… For Collaboration papers, we want to be sure that things are right before we share them publicly. We go through internal peer review. In my opinion this is much more thorough than journal review, and this shows how seriously the Collaboration take their science.

Unfortunately, setting up the review was also where we hit a hurdle—it took until July. I’m not entirely sure why there was a delay: I suspect it was partly because everyone was busy assembling things ahead of O1 and partly because there were various discussions amongst the high-level management about what exactly we should be aiming for. Working as part of a large collaboration can mean that you get to be involved in wonderful science, but it can means lots of bureaucracy and politics. However, in the intervening time, Living Reviews was back in operation.

The review team consisted of five senior people, each of whom had easily five times as much experience as I do, with expertise in each of the areas covered in the document. The chair of the review was Alan Weinstein, head of the Caltech LIGO Laboratory Astrophysics Group, who has an excellent eye for detail. Our aim was to produce the update for the start of O1 in September. (Spolier: We didn’t make it)

The review team discussed things amongst themselves and I got the first comments at the end of August. The consensus was that we should not just update the sky localization, but update everything too (including the structure of the document). This precipitated a flurry of conversations with the people who organise the schedules for the detectors, those who liaise with our partner astronomers on electromagnetic follow-up, and everyone who does sky localization. I was initially depressed that we wouldn’t make our start of O1 deadline; however, then something happened that altered my perspective.

On September 14, four days before the official start of O1, we made a detection. GW150914 would change everything.

First, we could no longer claim that binary neutron stars were expected to be our most common source—instead they became the source we expect would most commonly have an electromagnetic counterpart.

Second, we needed to be careful how we described engineering runs. GW150914 occurred in our final engineering run (ER8). Practically, there was difference between the state of the detector then and in O1. The point of the final engineering run was to get everything running smoothly so all we needed to do at the official start of O1 was open the champagne. However, we couldn’t make any claims about being able to make detections during engineering runs without being krass and letting the cat out of the bag. I’m rather pleased with the sentence

Engineering runs in the commissioning phase allow us to understand our detectors and analyses in an observational mode; these are not intended to produce astrophysical results, but that does not preclude the possibility of this happening.

I don’t know if anyone noticed the implication. (Checking my notes, this was in the September 18 draft, which shows how quickly we realised the possible significance of The Event).

Finally, since the start of observations proved to be interesting, and because the detectors were running so smoothly, it was decided to extend O1 from three months to four so that it would finish in January. No commissioning was going to be done over the holidays, so it wouldn’t affect the schedule. I’m not sure how happy the people who run the detectors were about working over this period, but they agreed to the plan. (No-one asked if we would be happy to run parameter estimation over the holidays).

After half-a-dozen drafts, the review team were finally happy with the document. It was now October 20, and time to proceed to the next step of review: circulation to the Collaboration.

Collaboration papers go through a sequence of stages. First they are circulated to the everyone for comments. This can be pointing out typos, suggesting references or asking questions about the analysis. This lasts two weeks. During this time, the results must also be presented on a Collaboration-wide teleconference. After comments are addressed, the paper is sent for examination Executive Committees of the LIGO and Virgo Collaborations. After approval from them (and the review team check any changes), the paper is circulated to the Collaboration again for any last comments and checking of the author list. At the same time it is sent to the Gravitational Wave International Committee, a group of all the collaborations interested in gravitational waves. This final stage is a week. Then you can you can submit the paper.

Peer review for the journal doesn’t seem to arduous in comparison does it?

Since things were rather busy with all the analysis of GW150914, the Observing Scenario took a little longer than usual to clear all these hoops. I presented to the Collaboration on Friday 13 November. (This was rather unlucky as I was at a workshop in Italy and I had to miss the tour of the underground Laboratori Nazionali del Gran Sasso). After addressing comments from everyone (the Executive Committees do read things carefully), I got the final sign-off to submit December 21. At least we made it before the end of O1.

Good things come…

This may sound like a tale of frustration and delay. However, I hope that it is more than that, and it shows how careful the Collaboration is. The Observing Scenarios is really a review: it doesn’t contain new science. The updated sky localization results are from studies which have appeared in peer-reviewed journals, and are based upon codes that have been separately reviewed. Despite this, every statement was examined and every number checked and rechecked, and every member of the Collaboration had opportunity to examine the results and comment on the document.

I guess this attention to detail isn’t surprising given that our work is based on measuring a change in length of one part in 1,000,000,000,000,000,000,000.

Since this is how we treat review articles, can you imagine how much scrutiny the Discovery Paper had? Everything had at least one extra layer of review, every number had to be signed-off individually by the appropriate review team, and there were so many comments on the paper that the editors had to switch to using a ticketing system we normally use for tracking bugs in our software. This level of oversight helped me to sleep a little more easily: there are six numbers in the abstract alone I could have potentially messed up.

Had a nightmare that all my numbers changed when I reran my analysis. Went back to sleep after remembering dreams aren't reviewed yet.

— Christopher Berry (@cplberry) January 14, 2016

Of course, all this doesn’t mean we can’t make mistakes…

Looking forward

The Living Reviews version was accepted January 22, just after the end of O1. We made had to make a couple of tweaks to correct tenses. The final version appeared February 8, in time to be the last paper of the pre-discovery era.

It is now time to be thinking about the next update! There are certainly a few things on the to-do list (perhaps even some news on LIGO-India). We are having a Collaboration meeting in a couple of weeks’ time, so hopefully I can start talking to people about it then. Perhaps it’ll be done by the start of O2? [update]

arXiv: 1304.0670 [gr-qc]
Journal: Living Reviews In Relativity; 19:1(39); 2016
Science summary: Planning for a Bright Tomorrow: Prospects for Gravitational-wave Astronomy with Advanced LIGO and Advanced Virgo
Bonus fact: This is the only paper whose arXiv ID I know by heart [update].

arXiv IDs

Papers whose arXiv numbers I know by heart are: 1304.0670, 1602.03840 (I count to other GW150914 companion papers from here), 1606.04856 and 1706.01812. These might tell you something about my reading habits.

The next version

Despite aiming for the start of O2, the next version wasn’t ready for submission until just after the end of O2, in September 2017. It was finally published (after an excpetionally long time in type-setting) in April 2018.

GW150914—The papers

February 23, 2016March 3, 2021 / CPLB / 3 Comments

In 2015 I made a resolution to write a blog post for each paper I had published. In 2016 I’ll have to break this because there are too many to keep up with. A suite of papers were prepared to accompany the announcement of the detection of GW150914 [bonus note], and in this post I’ll give an overview of these.

The papers

As well as the Discovery Paper published in Physical Review Letters [bonus note], there are 12 companion papers. All the papers are listed below in order of arXiv posting. My favourite is the Parameter Estimation Paper.

Subsequently, we have produced additional papers on GW150914, describing work that wasn’t finished in time for the announcement. The most up-to-date results are currently given in the O2 Catalogue Paper.

0. The Discovery Paper

Title: Observation of gravitational waves from a binary black hole merger
arXiv: 1602.03837 [gr-qc]
Journal: Physical Review Letters; 116(6):061102(16); 2016
LIGO science summary: Observation of gravitational waves from a binary black hole merger

This is the central paper that announces the observation of gravitational waves. There are three discoveries which are describe here: (i) the direct detection of gravitational waves, (ii) the existence of stellar-mass binary black holes, and (iii) that the black holes and gravitational waves are consistent with Einstein’s theory of general relativity. That’s not too shabby in under 11 pages (if you exclude the author list). Coming 100 years after Einstein first published his prediction of gravitational waves and Schwarzschild published his black hole solution, this is the perfect birthday present.

More details: The Discovery Paper summary

1. The Detector Paper

Title: GW150914: The Advanced LIGO detectors in the era of first discoveries
arXiv: 1602.03838 [gr-qc]
Journal: Physical Review Letters; 116(13):131103(12); 2016
LIGO science summary: GW150914: The Advanced LIGO detectors in the era of the first discoveries

This paper gives a short summary of how the LIGO detectors work and their configuration in O1 (see the Advanced LIGO paper for the full design). Giant lasers and tiny measurements, the experimentalists do some cool things (even if their paper titles are a little cheesy and they seem to be allergic to error bars).

More details: The Detector Paper summary

2. The Compact Binary Coalescence Paper

Title: GW150914: First results from the search for binary black hole coalescence with Advanced LIGO
arXiv: 1602.03839 [gr-qc]
Journal: Physical Review D; 93(12):122003(21); 2016
LIGO science summary: How we searched for merging black holes and found GW150914

Here we explain how we search for binary black holes and calculate the significance of potential candidates. This is the evidence to back up (i) in the Discovery Paper. We can potentially detect binary black holes in two ways: with searches that use templates, or with searches that look for coherent signals in both detectors without assuming a particular shape. The first type is also used for neutron star–black hole or binary neutron star coalescences, collectively known as compact binary coalescences. This type of search is described here, while the other type is described in the Burst Paper.

This paper describes the compact binary coalescence search pipelines and their results. As well as GW150914 there is also another interesting event, LVT151012. This isn’t significant enough to be claimed as a detection, but it is worth considering in more detail.

More details: The Compact Binary Coalescence Paper summary

3. The Parameter Estimation Paper

Title: Properties of the binary black hole merger GW150914
arXiv: 1602.03840 [gr-qc]
Journal: Physical Review Letters; 116(24):241102(19); 2016
LIGO science summary: The first measurement of a black hole merger and what it means

If you’re interested in the properties of the binary black hole system, then this is the paper for you! Here we explain how we do parameter estimation and how it is possible to extract masses, spins, location, etc. from the signal. These are the results I’ve been most heavily involved with, so I hope lots of people will find them useful! This is the paper to cite if you’re using our best masses, spins, distance or sky maps. The masses we infer are so large we conclude that the system must contain black holes, which is discovery (ii) reported in the Discovery Paper.

More details: The Parameter Estimation Paper summary

4. The Testing General Relativity Paper

Title: Tests of general relativity with GW150914
arXiv: 1602.03841 [gr-qc]
Journal: Physical Review Letters; 116(22):221101(19); 2016
LIGO science summary: Was Einstein right about strong gravity?

The observation of GW150914 provides a new insight into the behaviour of gravity. We have never before probed such strong gravitational fields or such highly dynamical spacetime. These are the sorts of places you might imagine that we could start to see deviations from the predictions of general relativity. Aside from checking that we understand gravity, we also need to check to see if there is any evidence that our estimated parameters for the system could be off. We find that everything is consistent with general relativity, which is good for Einstein and is also discovery (iii) in the Discovery Paper.

More details: The Testing General Relativity Paper summary

5. The Rates Paper

Title: The rate of binary black hole mergers inferred from Advanced LIGO observations surrounding GW150914
arXiv: 1602.03842 [astro-ph.HE]; 1606.03939 [astro-ph.HE]
Journal: Astrophysical Journal Letters; 833(1):L1(8); 2016; Astrophysical Journal Supplement Series; 227(2):14(11); 2016
LIGO science summary: The first measurement of a black hole merger and what it means

Given that we’ve spotted one binary black hole (plus maybe another with LVT151012), how many more are out there and how many more should we expect to find? We answer this here, although there’s a large uncertainty on the estimates since we don’t know (yet) the distribution of masses for binary black holes.

More details: The Rates Paper summary

6. The Burst Paper

Title: Observing gravitational-wave transient GW150914 with minimal assumptions
arXiv: 1602.03843 [gr-qc]
Journal: Physical Review D; 93(12):122004(20); 2016

What can you learn about GW150914 without having to make the assumptions that it corresponds to gravitational waves from a binary black hole merger (as predicted by general relativity)? This paper describes and presents the results of the burst searches. Since the pipeline which first found GW150914 was a burst pipeline, it seems a little unfair that this paper comes after the Compact Binary Coalescence Paper, but I guess the idea is to first present results assuming it is a binary (since these are tightest) and then see how things change if you relax the assumptions. The waveforms reconstructed by the burst models do match the templates for a binary black hole coalescence.

More details: The Burst Paper summary

7. The Detector Characterisation Paper

Title: Characterization of transient noise in Advanced LIGO relevant to gravitational wave signal GW150914
arXiv: 1602.03844 [gr-qc]
Journal: Classical & Quantum Gravity; 33(13):134001(34); 2016
LIGO science summary: How do we know GW150914 was real? Vetting a Gravitational Wave Signal of Astrophysical Origin
CQG+ post: How do we know LIGO detected gravitational waves? [featuring awesome cartoons]

Could GW150914 be caused by something other than a gravitational wave: are there sources of noise that could mimic a signal, or ways that the detector could be disturbed to produce something that would be mistaken for a detection? This paper looks at these problems and details all the ways we monitor the detectors and the external environment. We can find nothing that can explain GW150914 (and LVT151012) other than either a gravitational wave or a really lucky random noise fluctuation. I think this paper is extremely important to our ability to claim a detection and I’m surprised it’s not number 2 in the list of companion papers. If you want to know how thorough the Collaboration is in monitoring the detectors, this is the paper for you.

More details: The Detector Characterisation Paper summary

8. The Calibration Paper

Title: Calibration of the Advanced LIGO detectors for the discovery of the binary black-hole merger GW150914
arXiv: 1602.03845 [gr-qc]
Journal: Physical Review D; 95(6):062003(16); 2017
LIGO science summary: Calibration of the Advanced LIGO detectors for the discovery of the binary black-hole merger GW150914

Completing the triumvirate of instrumental papers with the Detector Paper and the Detector Characterisation Paper, this paper describes how the LIGO detectors are calibrated. There are some cunning control mechanisms involved in operating the interferometers, and we need to understand these to quantify how they effect what we measure. Building a better model for calibration uncertainties is high on the to-do list for improving parameter estimation, so this is an interesting area to watch for me.

More details: The Calibration Paper summary

9. The Astrophysics Paper

Title: Astrophysical implications of the binary black-hole merger GW150914
arXiv: 1602.03846 [astro-ph.HE]
Journal: Astrophysical Journal Letters; 818(2):L22(15); 2016
LIGO science summary: The first measurement of a black hole merger and what it means

Having estimated source parameters and rate of mergers, what can we say about astrophysics? This paper reviews results related to binary black holes to put our findings in context and also makes statements about what we could hope to learn in the future.

More details: The Astrophysics Paper summary

10. The Stochastic Paper

Title: GW150914: Implications for the stochastic gravitational wave background from binary black holes
arXiv: 1602.03847 [gr-qc]
Journal: Physical Review Letters; 116(13):131102(12); 2016
LIGO science summary: Background of gravitational waves expected from binary black hole events like GW150914

For every loud signal we detect, we expect that there will be many more quiet ones. This paper considers how many quiet binary black hole signals could add up to form a stochastic background. We may be able to see this background as the detectors are upgraded, so we should start thinking about what to do to identify it and learn from it.

More details: The Stochastic Paper summary

11. The Neutrino Paper

Title: High-energy neutrino follow-up search of gravitational wave event GW150914 with ANTARES and IceCube
arXiv: 1602.05411 [astro-ph.HE]
Journal: Physical Review D; 93(12):122010(15); 2016
LIGO science summary: Search for neutrinos from merging black holes

We are interested so see if there’s any other signal that coincides with a gravitational wave signal. We wouldn’t expect something to accompany a black hole merger, but it’s good to check. This paper describes the search for high-energy neutrinos. We didn’t find anything, but perhaps we will in the future (perhaps for a binary neutron star merger).

More details: The Neutrino Paper summary

12. The Electromagnetic Follow-up Paper

Title: Localization and broadband follow-up of the gravitational-wave transient GW150914
arXiv: 1602.08492 [astro-ph.HE]; 1604.07864 [astro-ph.HE]
Journal: Astrophysical Journal Letters; 826(1):L13(8); 2016; Astrophysical Journal Supplement Series; 225(1):8(15); 2016

As well as looking for coincident neutrinos, we are also interested in electromagnetic observations (gamma-ray, X-ray, optical, infra-red or radio). We had a large group of observers interesting in following up on gravitational wave triggers, and 25 teams have reported observations. This companion describes the procedure for follow-up observations and discusses sky localisation.

This work split into a main article and a supplement which goes into more technical details.

More details: The Electromagnetic Follow-up Paper summary

BEST. ARXIV. EVER!

We have 1602.03837 to 1602.03847 on #GravitationalWaves. A couple more to come. pic.twitter.com/HRdwcm60Mr

— Christopher Berry (@cplberry) February 12, 2016

The Discovery Paper

Synopsis: Discovery Paper
Read this if: You want an overview of The Event
Favourite part: The entire conclusion:

The LIGO detectors have observed gravitational waves from the merger of two stellar-mass black holes. The detected waveform matches the predictions of general relativity for the inspiral and merger of a pair of black holes and the ringdown of the resulting single black hole. These observations demonstrate the existence of binary stellar-mass black hole systems. This is the first direct detection of gravitational waves and the first observation of a binary black hole merger.

The Discovery Paper gives the key science results and is remarkably well written. It seems a shame to summarise it: you should read it for yourself! (It’s free).

The Detector Paper

Synopsis: Detector Paper
Read this if: You want a brief description of the detector configuration for O1
Favourite part: It’s short!

The LIGO detectors contain lots of cool pieces of physics. This paper briefly outlines them all: the mirror suspensions, the vacuum (the LIGO arms are the largest vacuum envelopes in the world and some of the cleanest), the mirror coatings, the laser optics and the control systems. A full description is given in the Advanced LIGO paper, but the specs there are for design sensitivity (it is also heavy reading). The main difference between the current configuration and that for design sensitivity is the laser power. Currently the circulating power in the arms is 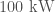$100~\mathrm{kW}$ , the plan is to go up to $750~\mathrm{kW}$ . This will reduce shot noise, but raises all sorts of control issues, such as how to avoid parametric instabilities.

The noise amplitude spectral density. The curves for the current observations are shown in red (dark for Hanford, light for Livingston). This is around a factor 3 better than in the final run of initial LIGO (green), but still a factor of 3 off design sensitivity (dark blue). The light blue curve shows the impact of potential future upgrades. The improvement at low frequencies is especially useful for high-mass systems like GW150914. Part of Fig. 1 of the Detector Paper.

The Compact Binary Coalescence Paper

Synopsis: Compact Binary Coalescence Paper
Read this if: You are interested in detection significance or in LVT151012
Favourite part: We might have found a second binary black hole merger

There are two compact binary coalescence searches that look for binary black holes: PyCBC and GstLAL. Both match templates to the data from the detectors to look for anything binary like, they then calculate the probability that such a match would happen by chance due to a random noise fluctuation (the false alarm probability or p-value [unhappy bonus note]). The false alarm probability isn’t the probability that there is a gravitational wave, but gives a good indication of how surprised we should be to find this signal if there wasn’t one. Here we report the results of both pipelines on the first 38.6 days of data (about 17 days where both detectors were working at the same time).

Both searches use the same set of templates to look for binary black holes [bonus note]. They look for where the same template matches the data from both detectors within a time interval consistent with the travel time between the two. However, the two searches rank candidate events and calculate false alarm probabilities using different methods. Basically, both searches use a detection statistic (the quantity used to rank candidates: higher means less likely to be noise), that is based on the signal-to-noise ratio (how loud the signal is) and a goodness-of-fit statistic. They assess the significance of a particular value of this detection statistic by calculating how frequently this would be obtained if there was just random noise (this is done by comparing data from the two detectors when there is not a coincident trigger in both). Consistency between the two searches gives us greater confidence in the results.

PyCBC’s detection statistic is a reweighted signal-to-noise ratio $\hat{\rho}_c$ which takes into account the consistency of the signal in different frequency bands. You can get a large signal-to-noise ratio from a loud glitch, but this doesn’t match the template across a range of frequencies, which is why this test is useful. The consistency is quantified by a reduced chi-squared statistic. This is used, depending on its value, to weight the signal-to-noise ratio. When it is large (indicating inconsistency across frequency bins), the reweighted signal-to-noise ratio becomes smaller.

To calculate the background, PyCBC uses time slides. Data from the two detectors are shifted in time so that any coincidences can’t be due to a real gravitational wave. Seeing how often you get something signal-like then tells you how often you’d expect this to happen due to random noise.

GstLAL calculates the signal-to-noise ratio and a residual after subtracting the template. As a detection statistic, it uses a likelihood ratio 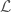$\mathcal{L}$ : the probability of finding the particular values of the signal-to-noise ratio and residual in both detectors for signals (assuming signal sources are uniformly distributed isotropically in space), divided by the probability of finding them for noise.

The background from GstLAL is worked out by looking at the likelihood ratio fro triggers that only appear in one detector. Since there’s no coincident signal in the other, these triggers can’t correspond to a real gravitational wave. Looking at their distribution tells you how frequently such things happen due to noise, and hence how probable it is for both detectors to see something signal-like at the same time.

The results of the searches are shown in the figure below.

Search results for PyCBC (left) and GstLAL (right). The histograms show the number of candidate events (orange squares) compare to the background. The black line includes GW150914 in the background estimate, the purple removes it (assuming that it is a signal). The further an orange square is above the lines, the more significant it is. Particle physicists like to quote significance in terms of $\sigma$ and for some reason we’ve copied them. The second most significant event (around $2\sigma$ ) is LVT151012. Fig. 7 from the Compact Binary Coalescence Paper.

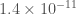GW150914 is the most significant event in both searches (it is the most significant PyCBC event even considering just single-detector triggers). They both find GW150914 with the same template values. The significance is literally off the charts. PyCBC can only calculate an upper bound on the false alarm probability of $< 2 \times 10^{-7}$ . GstLAL calculates a false alarm probability of $1.4 \times 10^{-11}$ , but this is reaching the level that we have to worry about the accuracy of assumptions that go into this (that the distribution of noise triggers in uniform across templates—if this is not the case, the false alarm probability could be about $10^3$ times larger). Therefore, for our overall result, we stick to the upper bound, which is consistent with both searches. The false alarm probability is so tiny, I don’t think anyone doubts this signal is real.

There is a second event that pops up above the background. This is LVT151012. It is found by both searches. Its signal-to-noise ratio is 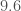$9.6$ , compared with GW150914’s 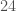$24$ , so it is quiet. The false alarm probability from PyCBC is 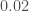$0.02$ , and from GstLAL is 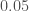$0.05$ , consistent with what we would expect for such a signal. LVT151012 does not reach the standards we would like to claim a detection, but it is still interesting.

Running parameter estimation on LVT151012, as we did for GW150914, gives beautiful results. If it is astrophysical in origin, it is another binary black hole merger. The component masses are lower, 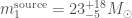$m_1^\mathrm{source} = 23^{+18}_{-5} M_\odot$ and $m_2^\mathrm{source} 13^{+4}_{-5} M_\odot$ (the asymmetric uncertainties come from imposing $m_1^\mathrm{source} \geq m_2^\mathrm{source}$ ); the chirp mass is $\mathcal{M} = 15^{+1}_{-1} M_\odot$ . 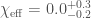The effective spin, as for GW150914, is close to zero $\chi_\mathrm{eff} = 0.0^{+0.3}_{-0.2}$ . The luminosity distance is $D_\mathrm{L} = 1100^{+500}_{-500}~\mathrm{Mpc}$ , meaning it is about twice as far away as GW150914’s source. I hope we’ll write more about this event in the future; there are some more details in the Rates Paper.

Is it random noise or is it a gravitational wave? LVT151012 remains a mystery. This candidate event is discussed in the Compact Binary Coalescence Paper (where it is found), the Rates Paper (which calculates the probability that it is extraterrestrial in origin), and the Detector Characterisation Paper (where known environmental sources fail to explain it). SPOILERS

The Parameter Estimation Paper

Synopsis: Parameter Estimation Paper
Read this if: You want to know the properties of GW150914’s source
Favourite part: We inferred the properties of black holes using measurements of spacetime itself!

The gravitational wave signal encodes all sorts of information about its source. Here, we explain how we extract this information to produce probability distributions for the source parameters. I wrote about the properties of GW150914 in my previous post, so here I’ll go into a few more technical details.

To measure parameters we match a template waveform to the data from the two instruments. The better the fit, the more likely it is that the source had the particular parameters which were used to generate that particular template. Changing different parameters has different effects on the waveform (for example, changing the distance changes the amplitude, while changing the relative arrival times changes the sky position), so we often talk about different pieces of the waveform containing different pieces of information, even though we fit the whole lot at once.

The shape of the gravitational wave encodes the properties of the source. This information is what lets us infer parameters. The example signal is GW150914. I made this explainer with Ban Farr and Nutsinee Kijbunchoo for the LIGO Magazine.

The waveform for a binary black hole merger has three fuzzily defined parts: the inspiral (where the two black holes orbit each other), the merger (where the black holes plunge together and form a single black hole) and ringdown (where the final black hole relaxes to its final state). Having waveforms which include all of these stages is a fairly recent development, and we’re still working on efficient ways of including all the effects of the spin of the initial black holes.

We currently have two favourite binary black hole waveforms for parameter estimation:

The first we refer to as EOBNR, short for its proper name of SEOBNRv2_ROM_DoubleSpin. This is constructed by using some cunning analytic techniques to calculate the dynamics (known as effective-one-body or EOB) and tuning the results to match numerical relativity (NR) simulations. This waveform only includes the effects of spins aligned with the orbital angular momentum of the binary, so it doesn’t allow us to measure the effects of precession (wobbling around caused by the spins).
The second we refer to as IMRPhenom, short for IMRPhenomPv2. This is constructed by fitting to the frequency dependence of EOB and NR waveforms. The dominant effects of precession of included by twisting up the waveform.

We’re currently working on results using a waveform that includes the full effects of spin, but that is extremely slow (it’s about half done now), so those results won’t be out for a while.

The results from the two waveforms agree really well, even though they’ve been created by different teams using different pieces of physics. This was a huge relief when I was first making a comparison of results! (We had been worried about systematic errors from waveform modelling). The consistency of results is partly because our models have improved and partly because the properties of the source are such that the remaining differences aren’t important. We’re quite confident that we’ve most of the parameters are reliably measured!

The component masses are the most important factor for controlling the evolution of the waveform, but we don’t measure the two masses independently. The evolution of the inspiral is dominated by a combination called the chirp mass, and the merger and ringdown are dominated by the total mass. For lighter mass systems, where we gets lots of inspiral, we measure the chirp mass really well, and for high mass systems, where the merger and ringdown are the loudest parts, we measure the total mass. GW150914 is somewhere in the middle. The probability distribution for the masses are shown below: we can compensate for one of the component masses being smaller if we make the other larger, as this keeps chirp mass and total mass about the same.

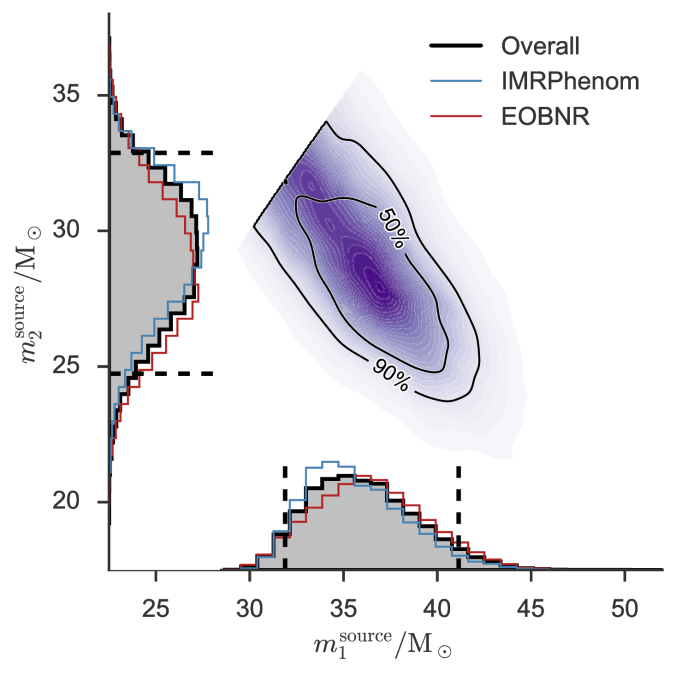
Estimated masses for the two black holes in the binary. Results are shown for the EOBNR waveform and the IMRPhenom: both agree well. The Overall results come from averaging the two. The dotted lines mark the edge of our 90% probability intervals. The sharp diagonal line cut-off in the two-dimensional plot is a consequence of requiring $m_1^\mathrm{source} \geq m_2^\mathrm{source}$ . Fig. 1 from the Parameter Estimation Paper.

To work out these masses, we need to take into account the expansion of the Universe. As the Universe expands, it stretches the wavelength of the gravitational waves. The same happens to light: visible light becomes redder, so the phenomenon is known as redshifting (even for gravitational waves). If you don’t take this into account, the masses you measure are too large. To work out how much redshift there is you need to know the distance to the source. The probability distribution for the distance is shown below, we plot the distance together with the inclination, since both of these affect the amplitude of the waves (the source is quietest when we look at it edge-on from the side, and loudest when seen face-on/off from above/below).

Estimated luminosity distance and binary inclination angle. An inclination of 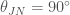$\theta_{JN} = 90^\circ$ means we are looking at the binary (approximately) edge-on. Results are shown for the EOBNR waveform and the IMRPhenom: both agree well. The Overall results come from averaging the two. The dotted lines mark the edge of our 90% probability intervals. Fig. 2 from the Parameter Estimation Paper.

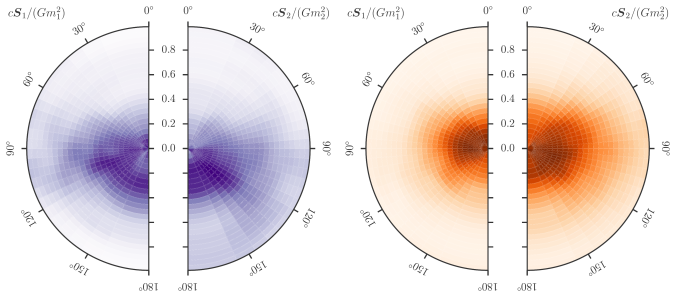
After the masses, the most important properties for the evolution of the binary are the spins. We don’t measure these too well, but the probability distribution for their magnitudes and orientations from the precessing IMRPhenom model are shown below. Both waveform models agree that the effective spin $\chi_\mathrm{eff}$ , which is a combination of both spins in the direction of the orbital angular momentum) is small. Therefore, either the spins are small or are larger but not aligned (or antialigned) with the orbital angular momentum. The spin of the more massive black hole is the better measured of the two.

Orientation and magnitudes of the two spins

Estimated orientation and magnitude of the two component spins from the precessing IMRPhenom model. The magnitude is between 0 and 1 and is perfectly aligned with the orbital angular momentum if the angle is 0. The distribution for the more massive black hole is on the left, and for the smaller black hole on the right. Part of Fig. 5 from the Parameter Estimation Paper.

The Testing General Relativity Paper

Synopsis: Testing General Relativity Paper
Read this if: You want to know more about the nature of gravity.
Favourite part: Einstein was right! (Or more correctly, we can’t prove he was wrong… yet)

The Testing General Relativity Paper is one of my favourites as it packs a lot of science in. Our first direct detection of gravitational waves and of the merger of two black holes provides a new laboratory to test gravity, and this paper runs through the results of the first few experiments.

Before we start making any claims about general relativity being wrong, we first have to check if there’s any weird noise present. You don’t want to have to rewrite the textbooks just because of an instrumental artifact. After taking out a good guess for the waveform (as predicted by general relativity), we find that the residuals do match what we expect for instrumental noise, so we’re good to continue.

I’ve written about a couple of tests of general relativity in my previous post: the consistency of the inspiral and merger–ringdown parts of the waveform, and the bounds on the mass of the graviton (from evolution of the signal). I’ll cover the others now.

The final part of the signal, where the black hole settles down to its final state (the ringdown), is the place to look to check that the object is a black hole and not some other type of mysterious dark and dense object. It is tricky to measure this part of the signal, but we don’t see anything odd. We can’t yet confirm that the object has all the properties you’d want to pin down that it is exactly a black hole as predicted by general relativity; we’re going to have to wait for a louder signal for this. This test is especially poignant, as Steven Detweiler, who pioneered a lot of the work calculating the ringdown of black holes, died a week before the announcement.

We can allow terms in our waveform (here based on the IMRPhenom model) to vary and see which values best fit the signal. If there is evidence for differences compared with the predictions from general relativity, we would have evidence for needing an alternative. 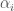Results for this analysis are shown below for a set of different waveform parameters $\hat{p}_i$ : the $\varphi_i$ parameters determine the inspiral, the $\alpha_i$ parameters determine the merger–ringdown and the $\beta_i$ parameters cover the intermediate regime. 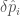If the deviation $\delta \hat{p}_i$ is zero, the value coincides with the value from general relativity. The plot shows what would happen if you allow all the variable to vary at once (the multiple results) and if you tried just that parameter on its own (the single results).

Probability distributions for waveform parameters. The single analysis only varies one parameter, the multiple analysis varies all of them, and the J0737-3039 result is the existing bound from the double pulsar. A deviation of zero is consistent with general relativity. Fig. 7 from the Testing General Relativity Paper.

Overall the results look good. Some of the single results are centred away from zero, but we think that this is just a random fluctuate caused by noise (we’ve seen similar behaviour in tests, so don’t panic yet). It’s not surprising the 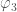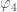$\varphi_3$ , $\varphi_4$ and $\varphi_{5l}$ all show this behaviour, as they are sensitive to similar noise features. 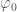These measurements are much tighter than from any test we’ve done before, except for the measurement of $\varphi_0$ which is better measured from the double pulsar (since we have lots and lots of orbits of that measured).

The final test is to look for additional polarizations of gravitational waves. These are predicted in several alternative theories of gravity. Unfortunately, because we only have two detectors which are pretty much aligned we can’t say much, at least without knowing for certain the location of the source. Extra detectors will be useful here!

In conclusion, we have found no evidence to suggest we need to throw away general relativity, but future events will help us to perform new and stronger tests.

The Rates Paper

Synopsis: Rates Paper
Read this if: You want to know how often binary black holes merge (and how many we’ll detect)
Favourite part: There’s a good chance we’ll have ten detections by the end of our second observing run (O2)

Before September 14, we had never seen a binary stellar-mass black hole system. We were therefore rather uncertain about how many we would see. We had predictions based on simulations of the evolution of stars and their dynamical interactions. These said we shouldn’t be too surprised if we saw something in O1, but that we shouldn’t be surprised if we didn’t see anything for many years either. We weren’t really expecting to see a black hole system so soon (the smart money was on a binary neutron star). However, we did find a binary black hole, and this happened right at the start of our observations! What do we now believe about the rate of mergers?

To work out the rate, you first need to count the number of events you have detected and then work out how sensitive you are to the population of signals (how many could you see out of the total).

Counting detections sounds simple: we have GW150914 without a doubt. However, what about all the quieter signals? If you have 100 events each with a 1% probability of being real, then even though you can’t say with certainty that anyone is an actual signal, you would expect one to be so. We want to work out how many events are real and how many are due to noise. Handily, trying to tell apart different populations of things when you’re not certain about individual members is a common problem is astrophysics (where it’s often difficult to go and check what something actually is), so there exists a probabilistic framework for doing this.

Using the expected number of real and noise events for a given detection statistic (as described in the Compact Binary Coalescence Paper), we count the number of detections and as a bonus, get a probability that each event is of astrophysical origin. There are two events with more than a 50% chance of being real: GW150914, where the probability is close to 100%, and LVT151012, where to probability is 84% based on GstLAL and 91% based on PyCBC.

By injecting lots of fake signals into some data and running our detection pipelines, we can work out how sensitive they are (in effect, how far away can they find particular types of sources). For a given number of detections, the more sensitive we are, the lower the actual rate of mergers should be (for lower sensitivity we would miss more, while there’s no hiding for higher sensitivity).

There is one final difficulty in working out the total number of binary black hole mergers: we need to know the distribution of masses, because our sensitivity depends on this. However, we don’t yet know this as we’ve only seen GW150914 and (maybe) LVT151012. Therefore, we try three possibilities to get an idea of what the merger rate could be.

We assume that binary black holes are either like GW150914 or like LVT151012. Given that these are our only possible detections at the moment, this should give a reasonable estimate. A similar approach has been used for estimating the population of binary neutron stars from pulsar observations [bonus note].
We assume that the distribution of masses is flat in the logarithm of the masses. This probably gives more heavy black holes than in reality (and so a lower merger rate)
We assume that black holes follow a power law like the initial masses of stars. This probably gives too many low mass black holes (and so a higher merger rate)

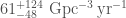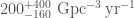The estimated merger rates (number of binary black hole mergers per volume per time) are then: 1. $83^{+168}_{-63}~\mathrm{Gpc^{-3}\,yr^{-1}}$ ; 2. $61^{+124}_{-48}~\mathrm{Gpc^{-3}\,yr^{-1}}$ , and 3. $200^{+400}_{-160}~\mathrm{Gpc^{-3}\,yr^{-1}}$ . There is a huge scatter, but the flat and power-law rates hopefully bound the true value.

We’ll pin down the rate better after a few more detections. How many more should we expect to see? Using the projected sensitivity of the detectors over our coming observing runs, we can work out the probability of making $N$ more detections. This is shown in the plot below. It looks like there’s about about a 10% chance of not seeing anything else in O1, but we’re confident that we’ll have 10 more by the end of O2, and 35 more by the end of O3! I may need to lie down…

The percentage chance of making 0, 10, 35 and 70 more detections of binary black holes as time goes on and detector sensitivity improves (based upon our data so far). This is a simplified version of part of Fig. 3 of the Rates Paper taken from the science summary.

The Burst Paper

Synopsis: Burst Paper
Read this if: You want to check what we can do without a waveform template
Favourite part: You don’t need a template to make a detection

When discussing what we can learn from gravitational wave astronomy, you can almost guarantee that someone will say something about discovering the unexpected. Whenever we’ve looked at the sky in a new band of the electromagnetic spectrum, we found something we weren’t looking for: pulsars for radio, gamma-ray burst for gamma-rays, etc. Can we do the same in gravitational wave astronomy? There may well be signals we weren’t anticipating out there, but will we be able to detect them? The burst pipelines have our back here, at least for short signals.

The burst search pipelines, like their compact binary coalescence partners, assign candidate events a detection statistic and then work out a probability associated with being a false alarm caused by noise. The difference is that the burst pipelines try to find a wider range of signals.

There are three burst pipelines described: coherent WaveBurst (cWB), which famously first found GW150914; omicron–LALInferenceBurst (oLIB), and BayesWave, which follows up on cWB triggers.

As you might guess from the name, cWB looks for a coherent signal in both detectors. It looks for excess power (indicating a signal) in a time–frequency plot, and then classifies candidates based upon their structure. There’s one class for blip glitches and resonance lines (see the Detector Characterisation Paper), these are all thrown away as noise; one class for chirp-like signals that increase in frequency with time, this is where GW150914 was found, and one class for everything else. cWB’s detection statistic $\eta_c$ is something like a signal-to-noise ratio constructed based upon the correlated power in the detectors. 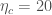The value for GW150914 was $\eta_c = 20$ , which is higher than for any other candidate. The false alarm probability (or p-value), folding in all three search classes, is $2\times 10^{-6}$ , which is pretty tiny, even if not as significant as for the tailored compact binary searches.

The oLIB search has two stages. First it makes a time–frequency plot and looks for power coincident between the two detectors. Likely candidates are then followed up by matching a sine–Gaussian wavelet to the data, using a similar algorithm to the one used for parameter estimation. It’s detection statistic is something like a likelihood ratio for the signal verses noise. It calculates a false alarm probability of about $2\times 10^{-6}$ too.

BayesWave fits a variable number of sine–Gaussian wavelets to the data. This can model both a signal (when the wavelets are the same for both detectors) and glitches (when the wavelets are independent). This is really clever, but is too computationally expensive to be left running on all the data. Therefore, it follows up on things highlighted by cWB, potentially increasing their significance. It’s detection statistic is the Bayes factor comparing the signal and glitch models. It estimates the false alarm probability to be about $7 \times 10^{-7}$ (which agrees with the cWB estimate if you only consider chirp-like triggers).

None of the searches find LVT151012. However, as this is a quiet, lower mass binary black hole, I think that this is not necessarily surprising.

cWB and BayesWave also output a reconstruction of the waveform. Reassuringly, this does look like binary black hole coalescence!

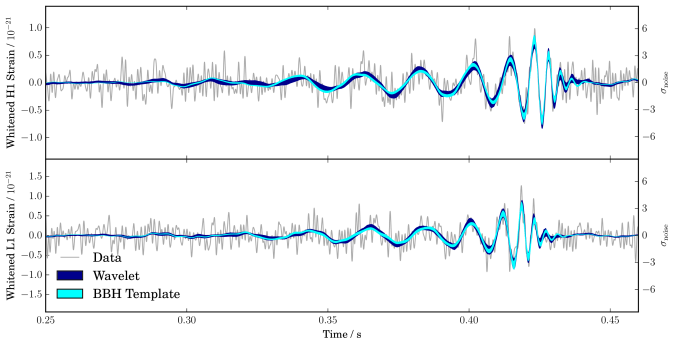
Estimated waveforms from different models

Gravitational waveforms from our analyses of GW150914. The wiggly grey line are the data from Hanford (top) and Livinston (bottom); these are analysed coherently. The plots show waveforms whitened by the noise power spectral density. The dark band shows the waveform reconstructed by BayesWave without assuming that the signal is from a binary black hole (BBH). The light bands show the distribution of BBH template waveforms that were found to be most probable from our parameter-estimation analysis. The two techniques give consistent results: the match between the two models is $94^{+2}_{-3}\%$ . Fig. 6 of the Parameter Estimation Paper.

The paper concludes by performing some simple fits to the reconstructed waveforms. For this, you do have to assume that the signal cane from a binary black hole. They find parameters roughly consistent with those from the full parameter-estimation analysis, which is a nice sanity check of our results.

The Detector Characterisation Paper

Synopsis: Detector Characteristation Paper
Read this if: You’re curious if something other than a gravitational wave could be responsible for GW150914 or LVT151012
Favourite part: Mega lightning bolts can cause correlated noise

The output from the detectors that we analyses for signals is simple. It is a single channel that records the strain. To monitor instrumental behaviour and environmental conditions the detector characterisation team record over 200,000 other channels. These measure everything from the alignment of the optics through ground motion to incidence of cosmic rays. Most of the data taken by LIGO is to monitor things which are not gravitational waves.

This paper examines all the potential sources of noise in the LIGO detectors, how we monitor them to ensure they are not confused for a signal, and the impact they could have on estimating the significance of events in our searches. It is amazingly thorough work.

There are lots of potential noise sources for LIGO. Uncorrelated noise sources happen independently at both sites, therefore they can only be mistaken for a gravitational wave if by chance two occur at the right time. Correlated noise sources effect both detectors, and so could be more confusing for our searches, although there’s no guarantee that they would cause a disturbance that looks anything like a binary black hole merger.

Sources of uncorrelated noise include:

Ground motion caused by earthquakes or ocean waves. These create wibbling which can affect the instruments, even though they are well isolated. This is usually at low frequencies (below 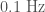$0.1~\mathrm{Hz}$ for earthquakes, although it can be higher if the epicentre is near), unless there is motion in the optics around (which can couple to cause higher frequency noise). There is a network of seismometers to measure earthquakes at both sites. There where two magnitude 2.1 earthquakes within 20 minutes of GW150914 (one off the coast of Alaska, the other south-west of Seattle), but both produced ground motion that is ten times too small to impact the detectors. There was some low frequency noise in Livingston at the time of LVT151012 which is associated with a period of bad ocean waves. however, there is no evidence that these could be converted to the frequency range associated with the signal.
People moving around near the detectors can also cause vibrational or acoustic disturbances. People are kept away from the detectors while they are running and accelerometers, microphones and seismometers monitor the environment.
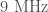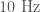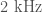Modulation of the lasers at $9~\mathrm{MHz}$ and $45~\mathrm{MHz}$ is done to monitor and control several parts of the optics. There is a fault somewhere in the system which means that there is a coupling to the output channel and we get noise across $10~\mathrm{Hz}$ to $2~\mathrm{kHz}$ , which is where we look for compact binary coalescences. Rai Weiss suggested shutting down the instruments to fix the source of this and delaying the start of observations—it’s a good job we didn’t. Periods of data where this fault occurs are flagged and not included in the analysis.
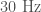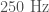Blip transients are a short glitch that occurs for unknown reasons. They’re quite mysterious. They are at the right frequency range ( $30~\mathrm{Hz}$ to $250~\mathrm{Hz}$ ) to be confused with binary black holes, but don’t have the right frequency evolution. They contribute to the background of noise triggers in the compact binary coalescence searches, but are unlikely to be the cause of GW150914 or LVT151012 since they don’t have the characteristic chirp shape.
A time–frequency plot of a blip glitch in LIGO-Livingston. Blip glitches are the right frequency range to be confused with binary coalescences, but don’t have the chirp-like structure. Blips are symmetric in time, whereas binary coalescences sweep up in frequency. Fig. 3 of the Detector Characterisation Paper.

Correlated noise can be caused by:

Electromagnetic signals which can come from lightning, solar weather or radio communications. This is measured by radio receivers and magnetometers, and its extremely difficult to produce a signal that is strong enough to have any impact of the detectors’ output. There was one strong (peak current of about 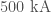$500~\mathrm{kA}$ ) lightning strike in the same second as GW150914 over Burkino Faso. However, the magnetic disturbances were at least a thousand times too small to explain the amplitude of GW150914.
Cosmic ray showers can cause electromagnetic radiation and particle showers. The particle flux become negligible after a few kilometres, so it’s unlikely that both Livingston and Hanford would be affected, but just in case there is a cosmic ray detector at Hanford. It has seen nothing suspicious.

All the monitoring channels give us a lot of insight into the behaviour of the instruments. Times which can be identified as having especially bad noise properties (where the noise could influence the measured output), or where the detectors are not working properly, are flagged and not included in the search analyses. Applying these vetoes mean that we can’t claim a detection when we know something else could mimic a gravitational wave signal, but it also helps us clean up our background of noise triggers. This has the impact of increasing the significance of the triggers which remain (since there are fewer false alarms they could be confused with). For example, if we leave the bad period in, the PyCBC false alarm probability for LVT151012 goes up from 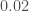$0.02$ to $0.14$ . 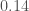The significance of GW150914 is so great that we don’t really need to worry about the effects of vetoes.

At the time of GW150914 the detectors were running well, the data around the event are clean, and there is nothing in any of the auxiliary channels that record anything which could have caused the event. The only source of a correlated signal which has not been rules out is a gravitational wave from a binary black hole merger. The time–frequency plots of the measured strains are shown below, and its easy to pick out the chirps.

Time–frequency plots for GW150914 as measured by Hanford (left) and Livingston (right). These show the characteristic increase in frequency with time of the chirp of a binary merger. The signal is clearly visible above the noise. Fig. 10 of the Detector Characterisation Paper.

The data around LVT151012 are significantly less stationary than around GW150914. There was an elevated noise transient rate around this time. This is probably due to extra ground motion caused by ocean waves. This low frequency noise is clearly visible in the Livingston time–frequency plot below. There is no evidence that this gets converted to higher frequencies though. None of the detector characterisation results suggest that LVT151012 has was caused by a noise artifact.

Time–frequency plots for LVT151012 as measured by Hanford (left) and Livingston (right). You can see the characteristic increase in frequency with time of the chirp of a binary merger, but this is mixed in with noise. The scale is reduced compared with for GW150914, which is why noise features appear more prominent. The band at low frequency in Livingston is due to ground motion; this is not present in Hanford. Fig. 13 of the Detector Characterisation Paper.

If you’re curious about the state of the LIGO sites and their array of sensors, you can see more about the physical environment monitors at pem.ligo.org.

The Calibration Paper

Synopsis: Calibration Paper
Read this if: You like control engineering or precision measurement
Favourite part: Not only are the LIGO detectors sensitive enough to feel the push from a beam of light, they are so sensitive that you have to worry about where on the mirrors you push

We want to measure the gravitational wave strain—the change in length across our detectors caused by a passing gravitational wave. What we actually record is the intensity of laser light out the output of our interferometer. (The output should be dark when the strain is zero, and the intensity increases when the interferometer is stretched or squashed). We need a way to convert intensity to strain, and this requires careful calibration of the instruments.

The calibration is complicated by the control systems. The LIGO instruments are incredibly sensitive, and maintaining them in a stable condition requires lots of feedback systems. These can impact how the strain is transduced into the signal readout by the interferometer. A schematic of how what would be the change in the length of the arms without control systems 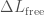$\Delta L_\mathrm{free}$ is changed into the measured strain 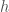$h$ is shown below. The calibration pipeline build models to correct for the effects of the control system to provide an accurate model of the true gravitational wave strain.

Model for how a differential arm length caused by a gravitational wave $\Delta L_\mathrm{free}$ or a photon calibration signal $x_\mathrm{T}^\mathrm{(PC)}$ is converted into the measured signal $h$ . Fig. 2 from the Calibration Paper.

To measure the different responses of the system, the calibration team make several careful measurements. The primary means is using photon calibration: an auxiliary laser is used to push the mirrors and the response is measured. The spots where the lasers are pointed are carefully chosen to minimise distortion to the mirrors caused by pushing on them. A secondary means is to use actuators which are parts of the suspension system to excite the system.

As a cross-check, we can also use two auxiliary green lasers to measure changes in length using either a frequency modulation or their wavelength. These are similar approaches to those used in initial LIGO. These go give consistent results with the other methods, but they are not as accurate.

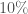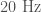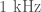Overall, the uncertainty in the calibration of the amplitude of the strain is less than $10\%$ between $20~\mathrm{Hz}$ and $1~\mathrm{kHz}$ , and the uncertainty in phase calibration is less than $10^\circ$ . These are the values that we use in our parameter-estimation runs. However, the calibration uncertainty actually varies as a function of frequency, with some ranges having much less uncertainty. We’re currently working on implementing a better model for the uncertainty, which may improve our measurements. Fortunately the masses, aren’t too affected by the calibration uncertainty, but sky localization is, so we might get some gain here. We’ll hopefully produce results with updated calibration in the near future.

The Astrophysics Paper

Synopsis: Astrophysics Paper
Read this if: You are interested in how binary black holes form
Favourite part: We might be able to see similar mass binary black holes with eLISA before they merge in the LIGO band [bonus note]

This paper puts our observations of GW150914 in context with regards to existing observations of stellar-mass black holes and theoretical models for binary black hole mergers. Although it doesn’t explicitly mention LVT151012, most of the conclusions would be just as applicable to it’s source, if it is real. I expect there will be rapid development of the field now, but if you want to catch up on some background reading, this paper is the place to start.

The paper contains lots of references to good papers to delve into. It also highlights the main conclusion we can draw in italics, so its easy to skim through if you want a summary. I discussed the main astrophysical conclusions in my previous post. We will know more about binary black holes and their formation when we get more observations, so I think it is a good time to get interested in this area.

The Stochastic Paper

Synopsis: Stochastic Paper
Read this if: You like stochastic backgrounds
Favourite part: We might detect a background in the next decade

A stochastic gravitational wave background could be created by an incoherent superposition of many signals. In pulsar timing, they are looking for a background from many merging supermassive black holes. Could we have a similar thing from stellar-mass black holes? The loudest signals, like GW150914, are resolvable, they stand out from the background. However, for every loud signal, there will be many quiet signals, and the ones below our detection threshold could form a background. Since we’ve found that binary black hole mergers are probably plentiful, the background may be at the high end of previous predictions.

The background from stellar-mass black holes is different than the one from supermassive black holes because the signals are short. While the supermassive black holes produce an almost constant hum throughout your observations, stellar-mass black hole mergers produce short chirps. Instead of having lots of signals that overlap in time, we have a popcorn background, with one arriving on average every 15 minutes. This might allow us to do some different things when it comes to detection, but for now, we just use the standard approach.

This paper calculates the energy density of gravitational waves from binary black holes, excluding the contribution from signals loud enough to be detected. This is done for several different models. The standard (fiducial) model assumes parameters broadly consistent with those of GW150914’s source, plus a particular model for the formation of merging binaries. There are then variations on the the model for formation, considering different time delays between formation and merger, and adding in lower mass systems consistent with LVT151012. All these models are rather crude, but give an idea of potential variations in the background. Hopefully more realistic distributions will be considered in the future. There is some change between models, but this is within the (considerable) statistical uncertainty, so predictions seems robust.

Models for a binary black hole stochastic background

Different models for the stochastic background of binary black holes. This is plotted in terms of energy density. The red band indicates the uncertainty on the fiducial model. The dashed line indicates the sensitivity of the LIGO and Virgo detectors after several years at design sensitivity. Fig. 2 of the Stochastic Paper.

After a couple of years at design sensitivity we may be able to make a confident detection of the stochastic background. The background from binary black holes is more significant than we expected.

If you’re wondering about if we could see other types of backgrounds, such as one of cosmological origin, then the background due to binary black holes could make detection more difficult. In effect, it acts as another source of noise, masking the other background. However, we may be able to distinguish the different backgrounds by measuring their frequency dependencies (we expect them to have different slopes), if they are loud enough.

The Neutrino Paper

Synopsis: Neutrino Paper
Read this if: You really like high energy neutrinos
Favourite part: We’re doing astronomy with neutrinos and gravitational waves—this is multimessenger astronomy without any form of electromagnetic radiation

There are multiple detectors that can look for high energy neutrinos. Currently, LIGO–Virgo Observations are being followed up by searches from ANTARES and IceCube. Both of these are Cherenkov detectors: they look for flashes of light created by fast moving particles, not the neutrinos themselves, but things they’ve interacted with. ANTARES searches the waters of the Mediterranean while IceCube uses the ice of Antarctica.

Within 500 seconds either side of the time of GW150914, ANTARES found no neutrinos and IceCube found three. These results are consistent with background levels (you would expect on average less than one and 4.4 neutrinos over that time from the two respectively). Additionally, none of the IceCube neutrinos are consistent with the sky localization of GW150914 (even though the sky area is pretty big). There is no sign of a neutrino counterpart, which is what we were expecting.

Subsequent non-detections have been reported by KamLAND, the Pierre Auger Observatory, Super-Kamiokande, Borexino and NOvA.

The Electromagnetic Follow-up Paper

Synopsis: Electromagnetic Follow-up Paper
Read this if: You are interested in the search for electromagnetic counterparts
Favourite part: So many people were involved in this work that not only do we have to abbreviate the list of authors (Abbott, B.P. et al.), but we should probably abbreviate the list of collaborations too (LIGO Scientific & Virgo Collaboration et al.)

This is the last of the set of companion papers to be released—it took a huge amount of coordinating because of all the teams involved. The paper describes how we released information about GW150914. This should not be typical of how we will do things going forward (i) because we didn’t have all the infrastructure in place on September 14 and (ii) because it was the first time we had something we thought was real.

The first announcement was sent out on September 16, and this contained sky maps from the Burst codes cWB and LIB. In the future, we should be able to send out automated alerts with a few minutes latency.

For the first alert, we didn’t have any results which assumed the the source was a binary, as the searches which issue triggers at low latency were only looking for lower mass systems which would contain a neutron star. I suspect we’ll be reprioritising things going forward. The first information we shared about the potential masses for the source was shared on October 3. Since this was the first detection, everyone was cautious about triple-checking results, which caused the delay. Revised false alarm rates including results from GstLAL and PyCBC were sent out October 20.

The final sky maps were shared January 13. This is when we’d about finished our own reviews and knew that we would be submitting the papers soon [bonus note]. Our best sky map is the one from the Parameter Estimation Paper. You might it expect to be more con straining than the results from the burst pipelines since it uses a proper model for the gravitational waves from a binary black hole. This is the case if we ignore calibration uncertainty (which is not yet included in the burst codes), then the 50% area is $48~\mathrm{deg}^2$ and the 90% area is $150~\mathrm{deg^2}$ . However, including calibration uncertainty, the sky areas are $150~\mathrm{deg^2}$ and $590~\mathrm{deg^2}$ at 50% and 90% probability respectively. Calibration uncertainty has the largest effect on sky area. All the sky maps agree that the source is in in some region of the annulus set by the time delay between the two detectors.

The different sky maps for GW150914 in an orthographic projection. The contours show the 90% region for each algorithm. The faint circles show lines of constant time delay 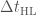$\Delta t_\mathrm{HL}$ between the two detectors. BAYESTAR rapidly computes sky maps for binary coalescences, but it needs the output of one of the detection pipelines to run, and so was not available at low latency. The LALInference map is our best result. All the sky maps are available as part of the data release. Fig. 2 of the Electromagnetic Follow-up Paper.

A timeline of events is shown below. There were follow-up observations across the electromagnetic spectrum from gamma-rays and X-rays through the optical and near infra-red to radio.

Timeline for observations of GW15014. The top (grey) band shows information about gravitational waves. The second (blue) band shows high-energy (gamma- and X-ray) observations. The third and fourth (green) bands show optical and near infra-red observations respectively. The bottom (red) band shows radio observations. Fig. 1 from the Electromagnetic Follow-up Paper.

Observations have been reported (via GCN notices) by

the Australian Square Kilometre Array Pathfinder (ASKAP) Collaboration
the BOOTES Collaboration
the Dark Energy Camera GW–EM Collaboration (Paper I, Paper II)
the Fermi GBM Collaboration
the Fermi LAT Collaboration
the Gravitational Wave Inaf Team (GRAWITA)
the INTEGRAL Collaboration
the Intermediate Palomar Transient Factory (iPTF) Collaboration (radio follow-up from the Jansky Very Large Array)
the Interplanetary Network (IPN)
the J-GEM Collaboration
the La Silla–Quest Survey
the Liverpool Telescope Collaboration
the Low Frequency Array (LOFAR) Collaboration
the MASTER Collaboration
the Monitor of All-sky X-ray Image (MAXI) Collaboration
the Murchison Wide-field Array (MWA) Collaboration
the Pan-STARRS Collaboration and the PESSTO Collaboration
the Pi of the Sky Collaboration
the SkyMapper Collaboration
the Swift Collaboration
the TAROT, Zadko, Algerian National Observatory and C2PU Collaboration
the TOROS Collaboration
the VISTA Collaboration

Together they cover an impressive amount of the sky as shown below. Many targeted the Large Magellanic Cloud before the knew the source was a binary black hole.

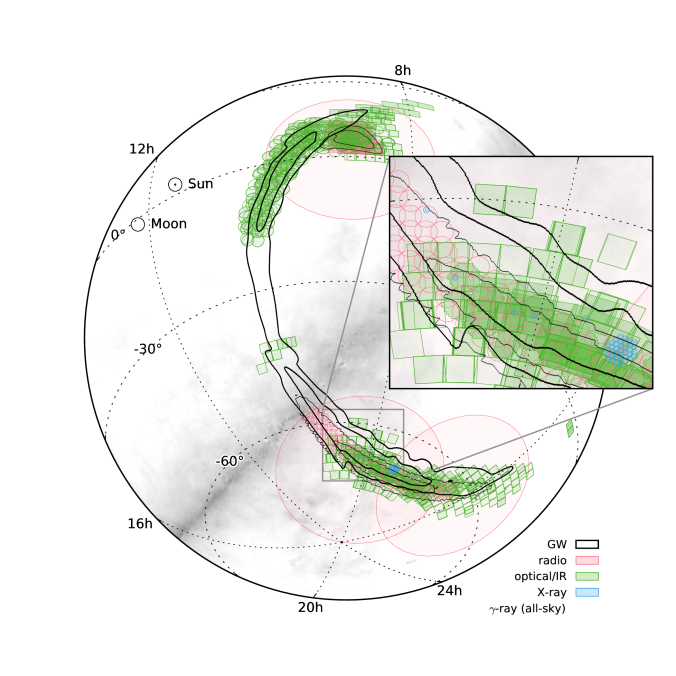
Footprints of observations compared with the 50% and 90% areas of the initially distributed (cWB: thick lines; LIB: thin lines) sky maps, also in orthographic projection. The all-sky observations are not shown. The grey background is the Galactic plane. Fig. 3 of the Electromagnetic Follow-up Paper.

Additional observations have been done using archival data by XMM-Newton and AGILE.

We don’t expect any electromagnetic counterpart to a binary black hole. No-one found anything with the exception of Fermi GBM. This has found a weak signal which may be coincident. More work is required to figure out if this is genuine (the statistical analysis looks OK, but some times you do have a false alarm). It would be a surprise if it is, so most people are sceptical. However, I think this will make people more interested in following up on our next binary black hole signal!

Bonus notes

Naming The Event

GW150914 is the name we have given to the signal detected by the two LIGO instruments. The “GW” is short for gravitational wave (not galactic worm), and the numbers give the date the wave reached the detectors (2015 September 14). It was originally known as G184098, its ID in our database of candidate events (most circulars sent to and from our observer partners use this ID). That was universally agreed to be terrible to remember. We tried to think of a good nickname for the event, but failed to, so rather by default, it has informally become known as The Event within the Collaboration. I think this is fitting given its significance.

LVT151012 is the name of the most significant candidate after GW150914, it doesn’t reach our criteria to claim detection (a false alarm rate of less than once per century), which is why it’s not GW151012. The “LVT” is short for LIGO–Virgo trigger. It took a long time to settle on this and up until the final week before the announcement it was still going by G197392. Informally, it was known as The Second Monday Event, as it too was found on a Monday. You’ll have to wait for us to finish looking at the rest of the O1 data to see if the Monday trend continues. If it does, it could have serious repercussions for our understanding of Garfield.

Following the publication of the O2 Catalogue Paper, LVT151012 was upgraded to GW151012, AND we decided to get rid of the LVT class as it was rather confusing.

Publishing in Physical Review Letters

Several people have asked me if the Discovery Paper was submitted to Science or Nature. It was not. The decision that any detection would be submitted to Physical Review was made ahead of the run. As far as I am aware, there was never much debate about this. Physical Review had been good about publishing all our non-detections and upper limits, so it only seemed fair that they got the discovery too. You don’t abandon your friends when you strike it rich. I am glad that we submitted to them.

Gaby González, the LIGO Spokesperson, contacted the editors of Physical Review Letters ahead of submission to let them know of the anticipated results. They then started to line up some referees to give confidential and prompt reviews.

The initial plan was to submit on January 19, and we held a Collaboration-wide tele-conference to discuss the science. There were a few more things still to do, so the paper was submitted on January 21, following another presentation (and a long discussion of whether a number should be a six or a two) and a vote. The vote was overwhelmingly in favour of submission.

We got the referee reports back on January 27, although they were circulated to the Collaboration the following day. This was a rapid turnaround! From their comments, I suspect that Referee A may be a particle physicist who has dealt with similar claims of first detection—they were most concerned about statistical significance; Referee B seemed like a relativist—they made comments about the effect of spin on measurements, knew about waveforms and even historical papers on gravitational waves, and I would guess that Referee C was an astronomer involved with pulsars—they mentioned observations of binary pulsars potentially claiming the title of first detection and were also curious about sky localization. While I can’t be certain who the referees were, I am certain that I have never had such positive reviews before! Referee A wrote

The paper is extremely well written and clear. These results are obviously going to make history.

Referee B wrote

This paper is a major breakthrough and a milestone in gravitational science. The results are overall very well presented and its suitability for publication in Physical Review Letters is beyond question.

and Referee C wrote

It is an honor to have the opportunity to review this paper. It would not be an exaggeration to say that it is the most enjoyable paper I’ve ever read. […] I unreservedly recommend the paper for publication in Physical Review Letters. I expect that it will be among the most cited PRL papers ever.

I suspect I will never have such emphatic reviews again [happy bonus note][unhappy bonus note].

Publishing in Physical Review Letters seems to have been a huge success. So much so that their servers collapsed under the demand, despite them adding two more in anticipation. In the end they had to quintuple their number of servers to keep up with demand. There were 229,000 downloads from their website in the first 24 hours. Many people remarked that it was good that the paper was freely available. However, we always make our papers public on the arXiv or via LIGO’s Document Control Center [bonus bonus note], so there should never be a case where you miss out on reading a LIGO paper!

Publishing the Parameter Estimation Paper

The reviews for the Parameter Estimation Paper were also extremely positive. Referee A, who had some careful comments on clarifying notation, wrote

This is a beautiful paper on a spectacular result.

Referee B, who commendably did some back-of-the-envelope checks, wrote

The paper is also very well written, and includes enough background that I think a decent fraction of it will be accessible to non-experts. This, together with the profound nature of the results (first direct detection of gravitational waves, first direct evidence that Kerr black holes exist, first direct evidence that binary black holes can form and merge in a Hubble time, first data on the dynamical strong-field regime of general relativity, observation of stellar mass black holes more massive than any observed to date in our galaxy), makes me recommend this paper for publication in PRL without hesitation.

Referee C, who made some suggestions to help a non-specialist reader, wrote

This is a generally excellent paper describing the properties of LIGO’s first detection.

Physical Review Letters were also kind enough to publish this paper open access without charge!

Publishing the Rates Paper

It wasn’t all clear sailing getting the companion papers published. Referees did give papers the thorough checking that they deserved. The most difficult review was of the Rates Paper. There were two referees, one astrophysics, one statistics. The astrophysics referee was happy with the results and made a few suggestions to clarify or further justify the text. The statistics referee has more serious complaints…

There are five main things which I think made the statistics referee angry. First, the referee objected to our terminology

While overall I’ve been impressed with the statistics in LIGO papers, in one respect there is truly egregious malpractice, but fortunately easy to remedy. It concerns incorrectly using the term “false alarm probability” (FAP) to refer to what statisticians call a p-value, a deliberately vague term (“false alarm rate” is similarly misused). […] There is nothing subtle or controversial about the LIGO usage being erroneous, and the practice has to stop, not just within this paper, but throughout the LIGO collaboration (and as a matter of ApJ policy).

I agree with this. What we call the false alarm probability is not the probability that the detection is a false alarm. It is not the probability that the given signal is noise rather that astrophysical, but instead it is the probability that if we only had noise that we would get a detection statistic as significant or more so. It might take a minute to realise why those are different. The former (the one we should call p-value) is what the search pipelines give us, but is less useful than the latter for actually working out if the signal is real. The probabilities calculated in the Rates Paper that the signal is astrophysical are really what you want.

p-values are often misinterpreted, but most scientists are aware of this, and so are cautious when they come across them

As a consequence of this complaint, the Collaboration is purging “false alarm probability” from our papers. It is used in most of the companion papers, as they were published before we got this report (and managed to convince everyone that it is important).

Second, we were lacking in references to existing literature

Regarding scholarship, the paper is quite poor. I take it the authors have written this paper with the expectation, or at least the hope, that it would be read […] If I sound frustrated, it’s because I am.

This is fair enough. The referee made some good suggestions to work done on inferring the rate of gamma-ray bursts by Loredo & Wasserman (Part I, Part II, Part III), as well as by Petit, Kavelaars, Gladman & Loredo on trans-Neptunian objects, and we made sure to add as much work as possible in revisions. There’s no excuse for not properly citing useful work!

Third, the referee didn’t understand how we could be certain of the distribution of signal-to-noise ratio 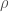$\rho$ without also worrying about the distribution of parameters like the black hole masses. The signal-to-noise ratio is inversely proportional to distance, and we expect sources to be uniformly distributed in volume. Putting these together (and ignoring corrections from cosmology) gives a distribution for signal-to-noise ratio of $p(\rho) \propto \rho^{-4}$ (Schulz 2011). This is sufficiently well known within the gravitational-wave community that we forgot that those outside wouldn’t appreciate it without some discussion. Therefore, it was useful that the referee did point this out.

Fourth, the referee thought we had made an error in our approach. They provided an alternative derivation which

if useful, should not be used directly without some kind of attribution

Unfortunately, they were missing some terms in their expressions. When these were added in, their approach reproduced our own (I had a go at checking this myself). Given that we had annoyed the referee on so many other points, it was tricky trying to convince them of this. Most of the time spent responding to the referees was actually working on the referee response and not on the paper.

Finally, the referee was unhappy that we didn’t make all our data public so that they could check things themselves. I think it would be great, and it will happen, it was just too early at the time.

LIGO Document Control Center

Papers in the LIGO Document Control Center are assigned a number starting with P (for “paper”) and then several digits. The Discover Paper’s reference is P150914. I only realised why this was the case on the day of submission.

The überbank

The set of templates used in the searches is designed to be able to catch binary neutron stars, neutron star–black hole binaries and binary neutron stars. It covers component masses from 1 to 99 solar masses, with total masses less than 100 solar masses. The upper cut off is chosen for computational convenience, rather than physical reasons: we do look for higher mass systems in a similar way, but they are easier to confuse with glitches and so we have to be more careful tuning the search. Since bank of templates is so comprehensive, it is known as the überbank. Although it could find binary neutron stars or neutron star–black hole binaries, we only discuss binary black holes here.

The template bank doesn’t cover the full parameter space, in particular it assumes that spins are aligned for the two components. This shouldn’t significantly affect its efficiency at finding signals, but gives another reason (together with the coarse placement of templates) why we need to do proper parameter estimation to measure properties of the source.

Alphabet soup

In the calculation of rates, the probabilistic means for counting sources is known as the FGMC method after its authors (who include two Birmingham colleagues and my former supervisor). The means of calculating rates assuming that the population is divided into one class to match each observation is also named for the initial of its authors as the KKL approach. The combined FGMCKKL method for estimating merger rates goes by the name alphabet soup, as that is much easier to swallow.

Multi-band gravitational wave astronomy

The prospect of detecting a binary black hole with a space-based detector and then seeing the same binary merger with ground-based detectors is especially exciting. My officemate Alberto Sesana (who’s not in LIGO) has just written a paper on the promise of multi-band gravitational wave astronomy. Black hole binaries like GW150914 could be spotted by eLISA (if you assume one of the better sensitivities for a detector with three arms). Then a few years to weeks later they merge, and spend their last moments emitting in LIGO’s band. The evolution of some binary black holes is sketched in the plot below.

Binary black hole mergers across the eLISA and LIGO frequency bands

The evolution of binary black hole mergers (shown in blue). The eLISA and Advanced LIGO sensitivity curves are shown in purple and orange respectively. As the black holes inspiral, they emit gravitational waves at higher frequency, shifting from the eLISa band to the LIGO band (where they merge). The scale at the top gives the approximate time until merger. Fig. 1 of Sesana (2016).

Seeing the signal in two bands can help in several ways. First it can increase our confidence in detection, potentially picking out signals that we wouldn’t otherwise. Second, it gives us a way to verify the calibration of our instruments. Third, it lets us improve our parameter-estimation precision—eLISA would see thousands of cycles, which lets it pin down the masses to high accuracy, these results can be combined with LIGO’s measurements of the strong-field dynamics during merger to give a fantastic overall picture of the system. Finally, since eLISA can measure the signal for a considerable time, it can well localise the source, perhaps just to a square degree; since we’ll also be able to predict when the merger will happen, you can point telescopes at the right place ahead of time to look for any electromagnetic counterparts which may exist. Opening up the gravitational wave spectrum is awesome!

The LALInference sky map

One of my jobs as part of the Parameter Estimation group was to produce the sky maps from our parameter-estimation runs. This is a relatively simple job of just running our sky area code. I had done it many times while were collecting our results, so I knew that the final versions were perfectly consistent with everything else we had seen. While I was comfortable with running the code and checking the results, I was rather nervous uploading the results to our database to be shared with our observational partners. I somehow managed to upload three copies by accident. D’oh! Perhaps future historians will someday look back at the records for G184098/GW150914 and wonder what was this idiot Christopher Berry doing? Probably no-one would every notice, but I know the records are there…

LIGO Magazine: Issue 7

September 12, 2015February 9, 2020 / CPLB / Leave a comment

It is an exciting time time in LIGO. The start of the first observing run (O1) is imminent. I think they just need to sort out a button that is big enough and red enough (or maybe gather a little more calibration data… ), and then it’s all systems go. Making the first direct detection of gravitational waves with LIGO would be an enormous accomplishment, but that’s not all we can hope to achieve: what I’m really interested in is what we can learn from these gravitational waves.

The LIGO Magazine gives a glimpse inside the workings of the LIGO Scientific Collaboration, covering everything from the science of the detector to what collaboration members like to get up to in their spare time. The most recent issue was themed around how gravitational-wave science links in with the rest of astronomy. I enjoyed it, as I’ve been recently working on how to help astronomers look for electromagnetic counterparts to gravitational-wave signals. It also features a great interview with Joseph Taylor Jr., one of the discoverers of the famous Hulse–Taylor binary pulsar. The back cover features an article I wrote about parameter estimation: an expanded version is below.

How does parameter estimation work?

Detecting gravitational waves is one of the great challenges in experimental physics. A detection would be hugely exciting, but it is not the end of the story. Having observed a signal, we need to work out where it came from. This is a job for parameter estimation!

How we analyse the data depends upon the type of signal and what information we want to extract. I’ll use the example of a compact binary coalescence, that is the inspiral (and merger) of two compact objects—neutron stars or black holes (not marshmallows). Parameters that we are interested in measuring are things like the mass and spin of the binary’s components, its orientation, and its position.

For a particular set of parameters, we can calculate what the waveform should look like. This is actually rather tricky; including all the relevant physics, like precession of the binary, can make for some complicated and expensive-to-calculate waveforms. The first part of the video below shows a simulation of the coalescence of a black-hole binary, you can see the gravitational waveform (with characteristic chirp) at the bottom.

We can compare our calculated waveform with what we measured to work out how well they fit together. If we take away the wave from what we measured with the interferometer, we should be left with just noise. We understand how our detectors work, so we can model how the noise should behave; this allows us to work out how likely it would be to get the precise noise we need to make everything match up.

To work out the probability that the system has a given parameter, we take the likelihood for our left-over noise and fold in what we already knew about the values of the parameters—for example, that any location on the sky is equally possible, that neutron-star masses are around 1.4 solar masses, or that the total mass must be larger than that of a marshmallow. For those who like details, this is done using Bayes’ theorem.

We now want to map out this probability distribution, to find the peaks of the distribution corresponding to the most probable parameter values and also chart how broad these peaks are (to indicate our uncertainty). Since we can have many parameters, the space is too big to cover with a grid: we can’t just systematically chart parameter space. Instead, we randomly sample the space and construct a map of its valleys, ridges and peaks. Doing this efficiently requires cunning tricks for picking how to jump between spots: exploring the landscape can take some time, we may need to calculate millions of different waveforms!

Having computed the probability distribution for our parameters, we can now tell an astronomer how much of the sky they need to observe to have a 90% chance of looking at the source, give the best estimate for the mass (plus uncertainty), or even figure something out about what neutron stars are made of (probably not marshmallow). This is the beginning of gravitational-wave astronomy!

Monty, Carla and the other samplers explore the probability landscape. Nutsinee Kijbunchoo drew the version for the LIGO Magazine.

Parameter estimation for binary neutron-star coalescences with realistic noise during the Advanced LIGO era

May 14, 2015February 9, 2020 / CPLB / Leave a comment

The first observing run (O1) of Advanced LIGO is nearly here, and with it the prospect of the first direct detection of gravitational waves. That’s all wonderful and exciting (far more exciting than a custard cream or even a chocolate digestive), but there’s a lot to be done to get everything ready. Aside from remembering to vacuum the interferometer tubes and polish the mirrors, we need to see how the data analysis will work out. After all, having put so much effort into the detector, it would be shame if we couldn’t do any science with it!

Parameter estimation

Since joining the University of Birmingham team, I’ve been busy working on trying to figure out how well we can measure things using gravitational waves. I’ve been looking at binary neutron star systems. We expect binary neutron star mergers to be the main source of signals for Advanced LIGO. We’d like to estimate how massive the neutron stars are, how fast they’re spinning, how far away they are, and where in the sky they are. Just published is my first paper on how well we should be able to measure things. This took a lot of hard work from a lot of people, so I’m pleased it’s all done. I think I’ve earnt a celebratory biscuit. Or two.

When we see something that looks like it could be a gravitational wave, we run code to analyse the data and try to work out the properties of the signal. Working out some properties is a bit trickier than others. Sadly, we don’t have an infinite number of computers, so it means it can take a while to get results. Much longer than the time to eat a packet of Jaffa Cakes…

The fastest algorithm we have for binary neutron stars is BAYESTAR. This takes the same time as maybe eating one chocolate finger. Perhaps two, if you’re not worried about the possibility of choking. BAYESTAR is fast as it only estimates where the source is coming from. It doesn’t try to calculate a gravitational-wave signal and match it to the detector measurements, instead it just looks at numbers produced by the detection pipeline—the code that monitors the detectors and automatically flags whenever something interesting appears. As far as I can tell, you give BAYESTAR this information and a fresh cup of really hot tea, and it uses Bayes’ theorem to work out how likely it is that the signal came from each patch of the sky.

To work out further details, we need to know what a gravitational-wave signal looks like and then match this to the data. This is done using a different algorithm, which I’ll refer to as LALInference. (As names go, this isn’t as cool as SKYNET). This explores parameter space (hopping between different masses, distances, orientations, etc.), calculating waveforms and then working out how well they match the data, or rather how likely it is that we’d get just the right noise in the detector to make the waveform fit what we observed. We then use another liberal helping of Bayes’ theorem to work out how probable those particular parameter values are.

It’s rather difficult to work out the waveforms, but some our easier than others. One of the things that makes things trickier is adding in the spins of the neutron stars. If you made a batch of biscuits at the same time you started a LALInference run, they’d still be good by the time a non-spinning run finished. With a spinning run, the biscuits might not be quite so appetising—I generally prefer more chocolate than penicillin on my biscuits. We’re working on speeding things up (if only to prevent increased antibiotic resistance).

In this paper, we were interested in what you could work out quickly, while there’s still chance to catch any explosion that might accompany the merging of the neutron stars. We think that short gamma-ray bursts and kilonovae might be caused when neutron stars merge and collapse down to a black hole. (I find it mildly worrying that we don’t know what causes these massive explosions). To follow-up on a gravitational-wave detection, you need to be able to tell telescopes where to point to see something and manage this while there’s still something that’s worth seeing. This means that using spinning waveforms in LALInference is right out, we just use BAYESTAR and the non-spinning LALInference analysis.

What we did

To figure out what we could learn from binary neutron stars, we generated a large catalogue of fakes signals, and then ran the detection and parameter-estimation codes on this to see how they worked. This has been done before in The First Two Years of Electromagnetic Follow-Up with Advanced LIGO and Virgo which has a rather delicious astrobites write-up. Our paper is the sequel to this (and features most of the same cast). One of the differences is that The First Two Years assumed that the detectors were perfectly behaved and had lovely Gaussian noise. In this paper, we added in some glitches. We took some real data™ from initial LIGO’s sixth science run and stretched this so that it matches the sensitivity Advanced LIGO is expected to have in O1. This process is called recolouring [bonus note]. We now have fake signals hidden inside noise with realistic imperfections, and can treat it exactly as we would real data. We ran it through the detection pipeline, and anything which was flagged as probably being a signal (we used a false alarm rate of once per century), was analysed with the parameter-estimation codes. We looked at how well we could measure the sky location and distance of the source, and the masses of the neutron stars. It’s all good practice for O1, when we’ll be running this analysis on any detections.

What we found

The flavour of noise (recoloured or Gaussian) makes no difference to how well we can measure things on average.
Sky-localization in O1 isn’t great, typically hundreds of square degrees (the median 90% credible region is 632 deg²), for comparison, the Moon is about a fifth of a square degree. This’ll make things interesting for the people with telescopes.
Probability that of a gravitational-wave signal coming from different points on the sky. The darker the red, the higher the probability. The star indicates the true location. This is one of the worst localized events from our study for O1. You can find more maps in the data release (including 3D versions), this is Figure 6 of Berry et al. (2015).
BAYESTAR does just as well as LALInference, despite being about 2000 times faster.
Sky localization (the size of the patch of the sky that we’re 90% sure contains the source location) varies with the signal-to-noise ratio (how loud the signal is). The approximate best fit is $\log_{10}(\mathrm{CR}_{0.9}/\mathrm{deg^2}) \approx -2 \log_{10}(\varrho) +5.06$ , where $\mathrm{CR}_{0.9}$ is the 90% sky area and $\varrho$ is the signal-to-noise ratio. The results for BAYESTAR and LALInference agree, as do the results with Gaussian and recoloured noise. This is Figure 9 of Berry et al. (2015).
We can’t measure the distance too well: the median 90% credible interval divided by the true distance (which gives something like twice the fractional error) is 0.85.
Because we don’t include the spins of the neutron stars, we introduce some error into our mass measurements. The chirp mass, a combination of the individual masses that we’re most sensitive to [bonus note], is still reliably measured (the median offset is 0.0026 of the mass of the Sun, which is tiny), but we’ll have to wait for the full spinning analysis for individual masses.
Fraction of events with difference between the mean estimated and true chirp mass smaller than a given value. There is an error because we are not including the effects of spin, but this is small. Again, the type of noise makes little difference. This is Figure 15 of Berry et al. (2015).

There’s still some work to be done before O1, as we need to finish up the analysis with waveforms that include spin. In the mean time, our results are all available online for anyone to play with.

arXiv: 1411.6934 [astro-ph.HE]
Journal: Astrophysical Journal; 904(2):114(24); 2015
Data release: The First Two Years of Electromagnetic Follow-Up with Advanced LIGO and Virgo
Favourite colour: Blue. No, yellow…

Notes

The colour of noise: Noise is called white if it doesn’t have any frequency dependence. We made ours by taking some noise with initial LIGO’s frequency dependence (coloured noise), removing the frequency dependence (making it white), and then adding in the frequency dependence of Advanced LIGO (recolouring it).

The chirp mass: Gravitational waves from a binary system depend upon the masses of the components, we’ll call these $m_1$ and $m_2$ . The chirp mass is a combination these that we can measure really well, as it determines the most significant parts of the shape of the gravitational wave. It’s given by

$\displaystyle \mathcal{M} = \frac{m_1^{3/5} m_2^{3/5}}{(m_1 + m_2)^{1/5}}$ .

We get lots of good information on the chirp mass, unfortunately, this isn’t too useful for turning back into the individual masses. For that we next extra information, for example the mass ratio $m_2/m_1$ . We can get this from less dominant parts of the waveform, but it’s not typically measured as precisely as the chirp mass, so we’re often left with big uncertainties.

Dirichlet process Gaussian mixture model

Gravitational-wave localization

Bonus notes

Writing

Sixth power

Treasure

Share this:

The papers

13. The Basic Physics Paper

14. The Precession Paper

15. The Systematics Paper

16. The Numerical Relativity Comparison Paper

The Basic Physics Paper

The Precession Paper

The Systematics Paper

The Numerical Relativity Comparison Paper

Bonus notes

Finches

The right answer

Formative experiences

Good things come…

Parameter key

Share this:

Going the distance

Bonus notes

Catalogue shopping

The gravitational-wave likelihood

Mergin’

Share this:

History

What we did

What we found

Bonus notes

How long?

Authorea

Share this:

Bonus notes

Review

Golden binaries

GW150914 results

The authors

Share this:

Bonus notes

Jargon

Parameter-estimation runs

Share this:

The Observing Scenarios

The path to publication

In the beginning

Updating sky localization

The review

Good things come…

Looking forward

arXiv IDs

The next version

Share this:

The papers

0. The Discovery Paper

1. The Detector Paper

2. The Compact Binary Coalescence Paper

3. The Parameter Estimation Paper

4. The Testing General Relativity Paper

5. The Rates Paper

6. The Burst Paper

7. The Detector Characterisation Paper

8. The Calibration Paper

9. The Astrophysics Paper

10. The Stochastic Paper

11. The Neutrino Paper

12. The Electromagnetic Follow-up Paper

The Discovery Paper

The Detector Paper

The Compact Binary Coalescence Paper

The Parameter Estimation Paper

The Testing General Relativity Paper

The Rates Paper

The Burst Paper

The Detector Characterisation Paper

The Calibration Paper

The Astrophysics Paper