Binary black hole mergers are the ultimate laboratory for testing gravity. The gravitational fields are strong, and things are moving at close to the speed of light. these extreme conditions are exactly where we expect our theories could breakdown, which is why we were so exciting by detecting gravitational waves from black hole coalescences. To accompany the first detection of gravitational waves, we performed several tests of Einstein’s theory of general relativity (it passed). This paper outlines the details of one of the tests, one that can be extended to include future detections to put Einstein’s theory to the toughest scrutiny.
One of the difficulties of testing general relativity is what do you compare it to? There are many alternative theories of gravity, but only a few of these have been studied thoroughly enough to give an concrete idea of what a binary black hole merger should look like. Even if general relativity comes out on top when compared to one alternative model, it doesn’t mean that another (perhaps one we’ve not thought of yet) can be ruled out. We need ways of looking for something odd, something which hints that general relativity is wrong, but doesn’t rely on any particular alternative theory of gravity.
The test suggested here is a consistency test. We split the gravitational-wave signal into two pieces, a low frequency part and a high frequency part, and then try to measure the properties of the source from the two parts. If general relativity is correct, we should get answers that agree; if it’s not, and there’s some deviation in the exact shape of the signal at different frequencies, we can get different answers. One way of thinking about this test is imagining that we have two experiments, one where we measure lower frequency gravitational waves and one where we measure higher frequencies, and we are checking to see if their results agree.
To split the waveform, we use a frequency around that of the last stable circular orbit: about the point that the black holes stop orbiting about each other and plunge together and merge [bonus note]. For GW150914, we used 132 Hz, which is about the same as the C an octave below middle C (a little before time zero in the simulation below). This cut roughly splits the waveform into the low frequency inspiral (where the two black hole are orbiting each other), and the higher frequency merger (where the two black holes become one) and ringdown (where the final black hole settles down).
We are fairly confident that we understand what goes on during the inspiral. This is similar physics to where we’ve been testing gravity before, for example by studying the orbits of the planets in the Solar System. The merger and ringdown are more uncertain, as we’ve never before probed these strong and rapidly changing gravitational fields. It therefore seems like a good idea to check the two independently [bonus note].
We use our parameter estimation codes on the two pieces to infer the properties of the source, and we compare the values for the mass and spin
of the final black hole. We could use other sets of parameters, but this pair compactly sum up the properties of the final black hole and are easy to explain. We look at the difference between the estimated values for the mass and spin,
and
, if general relativity is a good match to the observations, then we expect everything to match up, and
and
to be consistent with zero. They won’t be exactly zero because we have noise in the detector, but hopefully zero will be within the uncertainty region [bonus note]. An illustration of the test is shown below, including one of the tests we did to show that it does spot when general relativity is not correct.
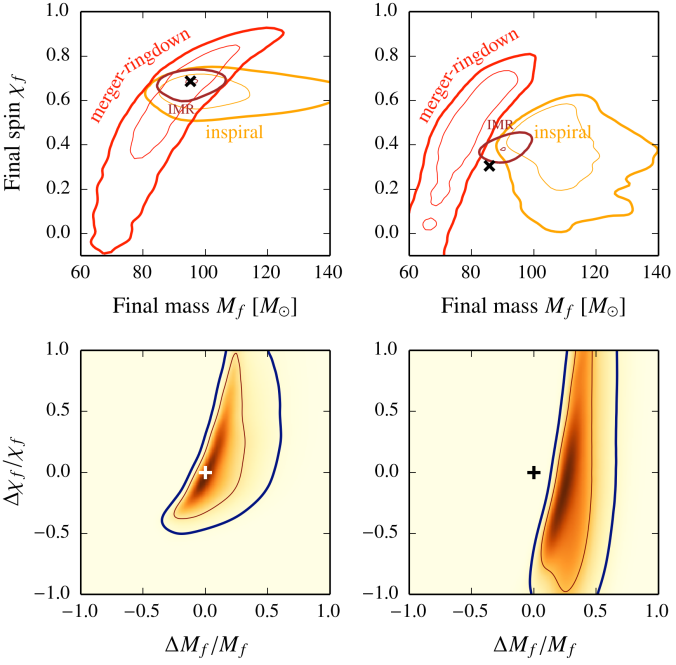
Results from the consistency test. The top panels show the outlines of the 50% and 90% credible levels for the low frequency (inspiral) part of the waveform, the high frequency (merger–ringdown) part, and the entire (inspiral–merger–ringdown, IMR) waveform. The bottom panel shows the fractional difference between the high and low frequency results. If general relativity is correct, we expect the distribution to be consistent with , indicated by the cross (+). The left panels show a general relativity simulation, and the right panel shows a waveform from a modified theory of gravity. Figure 1 of Ghosh et al. (2016).
A convenient feature of using and
to test agreement with relativity, is that you can combine results from multiple observations. By averaging over lots of signals, you can reduce the uncertainty from noise. This allows you to pin down whether or not things really are consistent, and spot smaller deviations (we could get precision of a few percent after about 100 suitable detections). I look forward to seeing how this test performs in the future!
arXiv: 1602.02453 [gr-qc]
Journal: Physical Review D; 94(2):021101(6); 2016
Favourite golden thing: Golden syrup sponge pudding
Bonus notes
Review
I became involved in this work as a reviewer. The LIGO Scientific Collaboration is a bit of a stickler when it comes to checking its science. We had to check that the test was coded up correctly, that the results made sense, and that calculations done and written up for GW150914 were all correct. Since most of the team are based in India [bonus note], this involved some early morning telecons, but it all went smoothly.
One of our checks was that the test wasn’t sensitive to exact frequency used to split the signal. If you change the frequency cut, the results from the two sections do change. If you lower the frequency, then there’s less of the low frequency signal and the measurement uncertainties from this piece get bigger. Conversely, there’ll be more signal in the high frequency part and so we’ll make a more precise measurement of the parameters from this piece. However, the overall results where you combine the two pieces stay about the same. You get best results when there’s a roughly equal balance between the two pieces, but you don’t have to worry about getting the cut exactly on the innermost stable orbit.
Golden binaries
In order for the test to work, we need the two pieces of the waveform to both be loud enough to allow us to measure parameters using them. This type of signals are referred to as golden. Earlier work on tests of general relativity using golden binaries has been done by Hughes & Menou (2015), and Nakano, Tanaka & Nakamura (2015). GW150914 was a golden binary, but GW151226 and LVT151012 were not, which is why we didn’t repeat this test for them.
GW150914 results
For The Event, we ran this test, and the results are consistent with general relativity being correct. The plots below show the estimates for the final mass and spin (here denoted rather than
), and the fractional difference between the two measurements. The points
is at the 28% credible level. This means that if general relativity is correct, we’d expect a deviation at this level to occur around-about 72% of the time due to noise fluctuations. It wouldn’t take a particular rare realisation of noise to cause the assume true value of
to be found at this probability level, so we’re not too suspicious that something is amiss with general relativity.

Results from the consistency test for The Event. The top panels final mass and spin measurements from the low frequency (inspiral) part of the waveform, the high frequency (post-inspiral) part, and the entire (IMR) waveform. The bottom panel shows the fractional difference between the high and low frequency results. If general relativity is correct, we expect the distribution to be consistent with , indicated by the cross. Figure 3 of the Testing General Relativity Paper.
The authors
Abhirup Ghosh and Archisman Ghosh were two of the leads of this study. They are both A. Ghosh at the same institution, which caused some confusion when compiling the LIGO Scientific Collaboration author list. I think at one point one of them (they can argue which) was removed as someone thought there was a mistaken duplication. To avoid confusion, they now have their full names used. This is a rare distinction on the Discovery Paper (I’ve spotted just two others). The academic tradition of using first initials plus second name is poorly adapted to names which don’t fit the typical western template, so we should be more flexible.